Giải mục 5 trang 35 SGK Toán 12 tập 1 - Chân trời sáng tạoVận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Lựa chọn câu để xem lời giải nhanh hơn
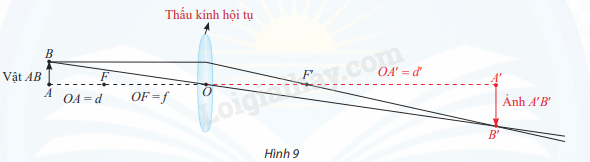
TH4 Trả lời câu hỏi Thực hành 4 trang 35 SGK Toán 12 Chân trời sáng tạo Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d’ là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d’ > 0, ảnh ảo thì d’ < 0). Ta có công thức: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d'}}}\) hay \(d' = \frac{{df}}{{d - f}}\) (Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187) Xét trường hợp f = 3, đặt x = d, y = d’. Ta có hàm số \(y = \frac{{3x}}{{x - 3}}\) và \(x \ne 3\). a) Khảo sát và vẽ đồ thị của hàm số trên. b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo. c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?
Phương pháp giải: a) Bước 1. Tìm tập xác định của hàm số Bước 2. Xét sự biến thiên của hàm số − Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số. − Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có). − Lập bảng biến thiên của hàm số. Bước 3. Vẽ đồ thị của hàm số − Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ − Vẽ các đường tiệm cận của đồ thị hàm số (nếu có). − Vẽ đồ thị hàm số. b) Ảnh ảo nếu d’ < 0 và ảnh thật nếu d’ > 0 c) Tìm giới hạn của d’ khi d tiến dần đến f Lời giải chi tiết: a) \(y = \frac{{3x}}{{x - 3}}\) Tập xác định: \(D = \mathbb{R}\backslash \{ 3\} \)
\(y' = \frac{{ - 9}}{{{{(x - 3)}^2}}} \le 0 \Leftrightarrow \forall x \in D\) nên hàm số nghịch biến trên \(D\)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x}}{{x - 3}} = 3;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (\frac{{3x}}{{x - 3}}) = 3\) nên y = 3 là tiệm cận ngang của đồ thị hàm số \(\mathop {\lim }\limits_{x \to {3^ + }} y = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{3x}}{{x - 3}} = + \infty ;\mathop {\lim }\limits_{x \to {3^ - }} y = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{3x}}{{x - 3}} = - \infty \) nên x = 3 là tiệm cận đứng của đồ thị hàm số
Khi x = 0 thì y = 0 nên (0;0) là giao điểm của y với trục Oy, Ox b) Để ảnh của vật là ảnh thật thì d’ > 0 hay y > 0 => x < 0 hoặc x > 3 hay d > 3 (do d là khoảng cách từ vật đến thấu kính nên d không thể nhỏ hơn 0) Để ảnh của vật là ảnh ảo thì d’ < 0 hay y < 0 => 0 < x < 3 hay 0 < d < 3 c) Khi vật tiến gần đến tiêu điểm thì khoảng cách từ ảnh đến thấu kính tiến dần tới vô cùng, ảnh của vật dần biến thành ảnh ảo TH5 Trả lời câu hỏi Thực hành 5 trang 35 SGK Toán 12 Chân trời sáng tạo Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 500\(c{m^3}\) với yêu cầu dùng ít vật liệu nhất. Chiều cao hộp phải là 2 cm, các kích thước khác là x, y với x > 0 và y > 0. a) Hãy biểu thị y theo x. b) Chứng tỏ rằng diện tích toàn phần của chiếc hộp là: \(S(x) = 500 + 4x + \frac{{1000}}{x}\). c) Lập bảng biến thiên của hàm số S(x) trên khoảng (0; \( + \infty \)). d) Kích thước của hộp là bao nhiêu thì dùng ít vật liệu nhất? (Làm tròn kết quả đến hàng phần mười.)
Phương pháp giải: a) Dựa vào công thức thể tích hình hộp chữ nhật V = xyh, từ đó suy ra mối liên hệ giữa x và y. b) Diện tích toàn phần của hình hộp chữ nhật: \({S_{tp}} = 2h(x + y) + 2xy\). c) Lập bảng biến thiên và tìm giá trị nhỏ nhất của \({S_{tp}}\) trên tập xác định. Lời giải chi tiết: a) \(y = \frac{{500}}{{2x}} = \frac{{250}}{x}\) b) Diện tích toàn phần của chiếc hộp là: \(S(x) = 2.2(x + y) + 2xy = 4(x + \frac{{250}}{x}) + 2.x.\frac{{250}}{x} = 500 + 4x + \frac{{1000}}{x}\) c) Tập xác định: \(D = (0; + \infty )\)
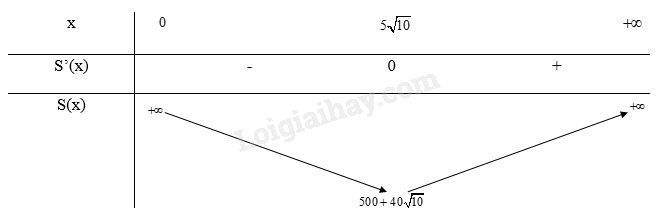
\(S'(x) = 4 - \frac{{1000}}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 5\sqrt {10} \\x = - 5\sqrt {10} (loai)\end{array} \right.\)
\(\mathop {\lim }\limits_{x \to + \infty } S(x) = \mathop {\lim }\limits_{x \to + \infty } (500 + 4x + \frac{{1000}}{x}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } S(x) = \mathop {\lim }\limits_{x \to - \infty } (500 + 4x + \frac{{1000}}{x}) = - \infty \) \(\mathop {\lim }\limits_{x \to {0^ + }} S(x) = \mathop {\lim }\limits_{x \to {0^ + }} (500 + 4x + \frac{{1000}}{x}) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} S(x) = \mathop {\lim }\limits_{x \to {0^ - }} (500 + 4x + \frac{{1000}}{x}) = - \infty \) Bảng biến thiên: d) Để S(x) nhỏ nhất thì x = \(15,8\)(cm) và \(y = \frac{{250}}{x} = \frac{{250}}{{5\sqrt {10} }} \approx 15,8\) (cm)
|