Bài 25. Động năng, thế năng trang 47, 48 SBT Vật lí 10 Kết nối tri thức với cuộc sốngMột vật có khối lượng 1 tấn đang chuyển động với tốc độ 72 km/h thì động năng của nó bằng
Lựa chọn câu để xem lời giải nhanh hơn
25.1 Một vật có khối lượng 1 tấn đang chuyển động với tốc độ 72 km/h thì động năng của nó bằng A. 7 200 J. B. 200 J. C. 200 kJ. D. 72 kJ. Phương pháp giải: Áp dụng công thức tính động năng: Wđ =\(\frac{1}{2}m{v^2}\). Trong đó:
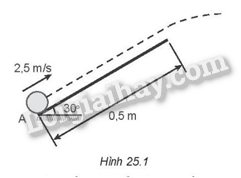
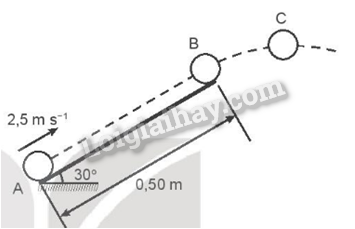
Lời giải chi tiết: Đổi m = 1 tấn = 1000 kg; v = 72 km/h = 20 m/s. Động năng của vật là: Wđ =\(\frac{1}{2}m{v^2}\)= \(\frac{1}{2}{.1000.20^2}\) = 200 kJ. Chọn đáp án C. 25.2 Một chiếc xe mô tô có khối lượng 220 kg đang chạy với tốc độ 14 m/s. Công cần thực hiện để tăng tốc xe lên tốc độ 19 m/s là bao nhiêu? A. 18 150 J. B. 21 560 J. C. 39 710 J. D. 2 750 J. Phương pháp giải: Động năng là năng lượng mà vật có được do chuyển động: Wđ = \(\frac{1}{2}m{v^2}\)có giá trị bằng công của lực làm cho vật chuyển động từ trạng thái đứng yên đến khi đạt được vận tốc đó. Lời giải chi tiết: Động năng của xe khi chạy với vận tốc 14 m/s là: Wđ1 =\(\frac{1}{2}mv_1^2\) = \(\frac{1}{2}{220.14^2}\) = 21560 J. Động năng của xe khi chạy với vận tốc 19 m/s là: Wđ2 =\(\frac{1}{2}mv_2^2\) = \(\frac{1}{2}{220.19^2}\) = 39710 J. Công cần thực hiện để tăng tốc độ xe từ 14 m/s lên tốc độ 19 m/s là: A = Wđ2 – Wđ1 = 39710 – 21560 = 18150 J. Chọn đáp án A. 25.3 Một vận động viên cử tạ nâng quả tạ khối lượng 200 kg từ mặt đất lên độ cao 1,5 m. Lấy gia tốc trọng trường là g = 9,8 m/s2. Độ tăng thế năng của tạ là A. 1962 J. B. 2 940 J. C. 800 J. D. 3 000 J. Phương pháp giải: Áp dụng công thức tính thế năng: Wt = P.h = mgh. Lời giải chi tiết: Chọn mốc thế năng là mặt đất. Khi đó độ tăng thế năng của tạ là: ∆W = mgh = 200.9,8.1,5 = 2940 J. Chọn đáp án B. 25.4 Một vật nặng 3 kg đang đứng yên trên mặt phẳng nhẵn nằm ngang thì bị tác dụng bởi một lực có độ lớn 15 N theo phương song song với mặt ngang trong thời gian 3 s. Tính: a) Vận tốc lớn nhất của vật. b) Công mà lực đã thực hiện. c) Động năng lớn nhất của vật. Phương pháp giải: a) Theo định luật II Newton: F = ma à a = \(\frac{F}{m}\) Áp dụng công thức để tính vận tốc của vật: v = v0 + at. b) Áp dụng công thức tính công của vật: A = F.s.cosα = F.s c) Áp dụng công thức tính động năng: Wđmax = \(\frac{1}{2}mv_{\max }^2\). Lời giải chi tiết: a) Theo định luật II Newton ta có: F = ma à a = \(\frac{F}{m}\)= \(\frac{{15}}{3}\)= 5 m/s2. Áp dụng công thức để tính vận tốc của vật: v = v0 + at = 0 + 5.3 = 15 m/s. Vậy vận tốc lớn nhất của vật là v = 15 m/s. b) Quãng đường mà vật đã đi được là: s = v0t + \(\frac{1}{2}a{t^2}\)= \(\frac{1}{2}{3.15^2}\)= 22,5 m. Khi đó công mà lực đã thực hiện là: A = F.s.cosα = F.s = 15.22,5 = 337,5 J. c) Áp dụng công thức tính động năng: Wđmax = \(\frac{1}{2}mv_{\max }^2\) = \(\frac{1}{2}{3.15^2}\) = 337,5 J. Vậy động năng lớn nhất của vật là: Wđmax = 337,5 J. 25.5 Có ba chiếc xe ô tô với khối lượng và vận tốc lần lượt là: Xe A: m, v. Xe B: \(\frac{m}{2}\), 3v. Xe C: 3m, \(\frac{v}{2}\). Thứ tự các xe theo thứ tự động năng tăng dần là A. (A, B, C). B. (B, C, A). C. (C, A, B). D. (C, B, A). Phương pháp giải: Áp dụng công thức tính động năng: Wđ =\(\frac{1}{2}m{v^2}\). Lời giải chi tiết: Động năng của xe A là: WđA = \(\frac{1}{2}{m_A}v_A^2\) = \(\frac{1}{2}m{v^2}\). Động năng của xe B là: WđB = \(\frac{1}{2}{m_B}v_B^2\) = \(\frac{1}{2}.\frac{m}{2}{(3v)^2}\) = \(\frac{9}{4}m{v^2}\) Động năng của xe C là: WđC = \(\frac{1}{2}{m_C}v_C^2\) = \(\frac{1}{2}.3m.{(\frac{v}{2})^2}\) =\(\frac{3}{8}m{v^2}\). => WđC < WđA < WđB. Chọn đáp án C. 25.6 Một máy bay nhỏ có khối lượng 690 kg đang chạy trên đường băng để cất cánh với động năng 25.103 J. a) Tính tốc độ của máy bay. b) Khi bắt đầu cất cánh, tốc độ máy bay tăng gấp 3 lần giá trị trên. Tính động năng của máy bay khi đó. Phương pháp giải: a) Từ công thức tính động năng: Wđ =\(\frac{1}{2}m{v^2}\) è v = \(\sqrt {\frac{{2{W_{\rm{d}}}}}{m}} \). b) Áp dụng công thức tính động năng: Wđ =\(\frac{1}{2}m{v^2}\). Trong đó: vs = 3vđ. Lời giải chi tiết: a) Từ công thức tính động năng: Wđ =\(\frac{1}{2}m{v^2}\) è v = \(\sqrt {\frac{{2{W_{\rm{d}}}}}{m}} \). Tốc độ của máy bay là: v = \(\sqrt {\frac{{{{2.25.10}^3}}}{{690}}} \)≈ 8,51 m/s. b) Theo đề ta có: vs = 3vđ. Động năng của máy bay khi bắt đầu cất cánh là: Wđ’ = \(\frac{1}{2}m{v_s}^2\)= \(\frac{1}{2}m{(3{v_{\rm{d}}})^2}\)≈ 224864,41 J. 25.7 Một quả bóng khối lượng 200 g được đẩy với vận tốc ban đầu 2,5 m/s lên một mặt phẳng nghiêng, nhẵn, dài 0,5 m, hợp với phương nằm ngang góc 30° (Hình 25.1). Quả bóng chuyền động như một vật bị ném. Bỏ qua lực cản của không khí và lấy g = 9,8 m/s2. Tìm giá trị nhỏ nhất của động năng quả bóng trong quá trình nó chuyển động.
Phương pháp giải: Áp dụng định luật bảo toàn cơ năng: Vì bỏ qua mọi lực cản nên cơ năng tại A bằng cơ năng tại B: WA = WB. Trong đó động năng được tính bằng công thức: Wđ =\(\frac{1}{2}m{v^2}\). Và thế năng được tính bằng công thức: Wt = P.h = mgh. Động năng cực tiểu thì bằng: Wđmin = \(\frac{1}{2}m{v_{\min }}\). Lời giải chi tiết:
Chọn mốc thế năng là vị trí ban đầu của quả bóng trên mặt phẳng nghiêng. Đổi m = 200 g = 0,2 kg. Vì bỏ qua mọi lực cản nên cơ năng tại A bằng cơ năng tại B: WA = WB. =>\(\frac{1}{2}mv_A^2 = \frac{1}{2}mv_B^2 + mg{h_B}\) => \(\frac{1}{2}0,2.2,{5^2} = \frac{1}{2}.0,2.v_B^2 + 0,2.9,8.0,5.\sin {30^o}\) => vB ≈ 1,16 m/s. Tại B, coi vật chuyển động bị ném nghiêng 30o so với phương ngang. Vận tốc theo phương nằm ngang: vBx = vBcos30o. Vận tốc theo phương này không thay đổi trong quá trình chuyển động. Vận tốc theo phương thẳng đứng: vBy = vBsin30o. Ở điểm cao nhất tại C thì: vC = vCx + vCy Mà: vCy = 0 => vC = vCx = vBcos30o. Động năng cực tiểu bằng: Wđmin = \(\frac{1}{2}m{({v_B}\cos {30^o})^2}\)≈ 0,10 J. 25.8 Ngày 11/7/1979, tàu vũ trụ Skylab quay trở lại bầu khí quyền của Trái Đất và bị nổ thành nhiều mảnh. Mảnh vỡ lớn nhất có khối lượng 1770 kg và nó va chạm vào bề mặt trái đất với tốc độ 120 m/s. Tính động năng của mảnh vỡ này. Phương pháp giải: Áp dụng công thức tính động năng: Wđ =\(\frac{1}{2}m{v^2}\). Lời giải chi tiết: Động năng của mảnh vỡ được tính theo công thức: Wd = \(\frac{1}{2}m{v^2}\)= \(\frac{1}{2}{.1770.120^2}\)≈ 12,744.106 J. 25.9 Một em bé có khối lượng 4,2 kg đang nằm trên giường có độ cao 40 cm so với mặt sàn thì được bố bế lên đến độ cao 1,5 m so với mặt sàn. Lấy gia tốc trọng trường g= 9,8 m/s2. Tính công tối thiểu mà người bố đã thực hiện. Phương pháp giải: Thế năng của vật ở độ cao h có độ lớn bằng công của lực dùng để nâng vật lên độ cao này: A = F.s = P.h = m.g.h = Wt. Vì vậy công tối thiểu mà người đó thực hiện để bé em bé từ độ cao 40 cm lên đến độ cao 1,5 m so với mặt sàn là: A = Wt2 – Wt1 Lời giải chi tiết: Chọn mốc thế năng là mặt đất. Đổi 40 cm = 0,4 m. Công tối thiểu mà người đó thực hiện để bé em bé từ độ cao 40 cm lên đến độ cao 1,5 m so với mặt sàn là: A = Wt2 – Wt1 = mgh2 – mgh1 = mg(h2 – h1) = 4,2.9,8.(1,5 – 0,4) = 45,276 J.
|