Bài 5. Tốc độ và vận tốc trang 9, 10 SBT Vật lí 10 Kết nối tri thức với cuộc sốngMột người chuyển động thẳng có độ dịch chuyển d1 tại thời điểm t1 và độ dịch chuyển d2 tại thời điểm t2. Vận tốc trung bình của vật trong khoảng thời gian từ t1 đến t2 là:
Lựa chọn câu để xem lời giải nhanh hơn
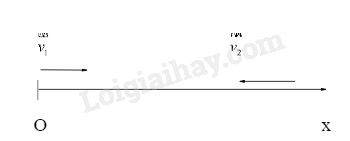
5.1 Một người chuyển động thẳng có độ dịch chuyển d1 tại thời điểm t1 và độ dịch chuyển d2 tại thời điểm t2. Vận tốc trung bình của vật trong khoảng thời gian từ t1 đến t2 là: A. \({v_{tb}} = \frac{{{d_1} - {d_2}}}{{{t_1} + {t_2}}}\) B. \({v_{tb}} = \frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\) C. \({v_{tb}} = \frac{{{d_1} + {d_2}}}{{{t_2} - {t_1}}}\) D. \(\frac{1}{2}\left( {\frac{{{d_1}}}{{{t_1}}} + \frac{{{d_2}}}{{{t_2}}}} \right)\) Phương pháp giải: Sử dụng công thức tính vận tốc trung bình Lời giải chi tiết: \({v_{tb}} = \frac{{\Delta x}}{{\Delta t}} = \frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\) + \(\Delta x\): Độ dời (m) + \(\Delta t\): Thời gian chuyển động (s) 5.2 Tính chất nào sau đây là của vận tốc, không phải của tốc độ của một chuyển động? A. Đặc trưng cho sự nhanh chậm của chuyển động. B. Có đơn vị là km/h C. Không thể có độ lớn bằng 0. D. Có phương xác định. Phương pháp giải: Tốc độ trung bình là đại lượng vô hướng có ý nghĩa vật lý đặc trưng cho độ nhanh hay chậm của chuyển động. Vận tốc trung bình là đại lượng vật lý có hướng (véctơ) cùng hướng với độ dời \(\overrightarrow {\Delta x} \)được xác định trong khoảng thời gian \(\Delta t\). Lời giải chi tiết: A sai vì cả tốc độ trung bình và vận tốc trung bình đều đặc trưng cho sự nhanh chậm của chuyển động. B sai vì cả tốc độ trung bình và vận tốc trung bình đều có thể có đơn vị là km/h. C sai vì cả tốc độ trung bình và vận tốc trung bình đều có thể có độ lớn bằng 0. D đúng vì vận tốc trung bình là đại lượng vật lý có hướng (véctơ) cùng hướng với độ dời \(\overrightarrow {\Delta x} \)còn tốc độ trung bình là đại lượng vô hướng. Chọn đáp án D 5.3 Một người tập thể dục chạy trên đường thẳng trong 10 min. Trong 4 min đầu chạy với vận tốc 4m/s, trong thời gian còn lại giảm vận tốc còn 3 m/s. Tính quãng đường chạy, độ dịch chuyển, tốc độ trung bình và vận tốc trung bình trên cả quãng đường chạy. Phương pháp giải: - Chuyển động theo một chiều nên độ dời trùng với quãng đường chạy được của người đó. Biểu thức tính quãng đường: s = v.t - Chuyển động chỉ theo một chiều nên trong cả thời gian chạy vận tốc trung bình bằng tốc độ trung bình Biểu thức tính tốc độ trung bình: v = \(\frac{s}{t}\) Trong đó: + v: tốc độ chuyển động của vật (m/s) + s: quãng đường đi được của vật (m) + t: thời gian đi được quãng đường s của vật (s) Lời giải chi tiết: Tóm tắt: t = 10 min = 600 s t1 = 4 min = 240s; v1= 4 m/s t2 = 600s – 240s = 360s; v2 = 3 m/s s = = ? m; v = vtb = ? m/s Lời giải: Chọn trục Ox trùng với đường chạy và có gốc là điểm xuất phát của người. Vì chuyển động theo một chiều nên độ dời trùng với quãng đường chạy được của người đó. Quãng đường chạy trong thời gian t2: s2 = 3.360 = 1080 m Quãng đường chạy trong 10 min là: s = s1 + s2 = 960 + 1080 = 2040 m Vì chuyển động chỉ theo một chiều nên trong cả thời gian chạy vận tốc trung bình bằng tốc độ trung bình và bằng: vtb = \(\frac{s}{t}\) = = 3.4m/s 5.4 Một người bơi dọc trong bể bơi dài 50 m. Bơi từ đầu bê đến cuối bể hết 20 s, bơi tiếp từ cuối bể quay về đầu bể hết 22 s. Xác định tốc độ trung bình và vận tốc trung bình trong 3 trường hợp sau: a) Bơi từ đầu để đến cuối bể. b) Bơi từ cuối bể về đầu bể. c) Bơi cả đi lẫn về. Phương pháp giải: Biểu thức tính tốc độ trung bình: v = \(\frac{s}{t}\) Biểu thức tính vận tốc trung bình: vtb = \(\frac{{\Delta x}}{{\Delta t}}\) Trong đó: + v: tốc độ chuyển động của vật (m/s) + s: quãng đường đi được của vật (m) + t: thời gian đi được quãng đường s của vật (s) + \(\Delta x\): Độ dời + \(\Delta t\): thời gian chuyển động khoảng Lời giải chi tiết: Chọn trục Ox trùng với chiều dọc của bể bơi, gốc O là điểm xuất phát như hình vẽ:
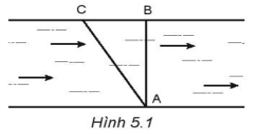
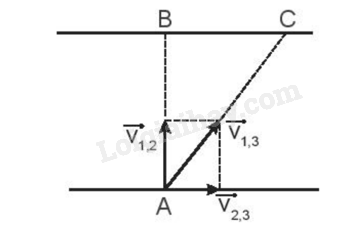
a) Khi người đó bơi từ đầu bể đến cuối bể thì: s = 50 m; độ dời \(\Delta {x_1}\) = +50 m; \(\Delta {t_1}\)= 20s Tốc độ trung bình: v1 = \(\frac{s}{{\Delta {t_1}}}\) = \(\frac{{50}}{{20}}\)= 2,5 m/s vtb1 = \(\frac{{\Delta {x_1}}}{{\Delta {t_1}}}\) = \(\frac{{50}}{{20}}\) = 2,5 m/s b) Khi người đó bơi từ cuối bể về đầu bể thì: s = 50 m; độ dời \(\Delta {x_2}\) = -50 m; \(\Delta {t_2}\) = 22s Tốc độ trung bình: v2 = \(\frac{s}{{\Delta {t_2}}}\) = \(\frac{{50}}{{22}}\) = 2,28 m/s vtb2 = \(\frac{{\Delta {x_2}}}{{\Delta {t_2}}}\) = \(\frac{{ - 50}}{{22}}\) = - 2,28 m/s c) Khi người đó bơi cả đi lẫn về thì s = 100 m; độ dời \(\Delta {x_3}\) = 0 m; \(\Delta {t_3}\) = 42s Tốc độ trung bình: v3 = \(\frac{s}{{\Delta {t_3}}}\) = \(\frac{{100}}{{42}}\) = 2,38 m/s vtb2 = \(\frac{{\Delta {x_3}}}{{\Delta {t_3}}}\) = \(\frac{0}{{42}}\) = 0 m/s 5.5 Hai ô tô khởi hành cùng một lúc từ hai địa điểm cách nhau 40 km. Nếu chúng đi ngược chiều thì sau 24 min sẽ gặp nhau. Nếu chúng đi cùng chiều thì sau 2h sẽ gặp nhau. Tính vận tốc mỗi xe. Phương pháp giải: Sử dụng công thức cộng vận tốc được xác định bằng biểu thức: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) Trong đó: + Số 1: gắn với vật cần tính vận tốc + Số 2: gắn với hệ quy chiếu là các vật chuyển động + Số 3: gắn với hệ quy chiếu là các vật đứng yên + v12: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối + v23: vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo + v13: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tuyệt đối. Lời giải chi tiết: Số 1 xe A; số 2 xe B; số 3 mặt đường; t1 = 24 phút = 0,4 h; t2 = 2 h \(\overrightarrow {{v_{13}}} \)là vận tốc của xe A so với đường. \(\overrightarrow {{v_{12}}} \)là vận tốc của xe A so với xe B. \(\overrightarrow {{v_{23}}} \)là vận tốc của xe B so với đường. Khi đi ngược chiều: v13 = v12 – v23 => v12 = v13 + v23 = \(\frac{{40}}{{0,4}}\) = 100 km/h ⇨ v13 + v23 = 100 (1) Khi hai xe chuyển động cùng chiều: v13 = v’12 + v23 => v’12 = v13 – v23 = \(\frac{{40}}{{0,2}}\) = 20 km/h ⇨ v13 – v23 = 20 (2) Từ (1) và (2) => v13 = 60 km/h; v23 = 40 km/h Vậy vận tốc của mỗi xe lần lượt là 60 km/h và 40 km/h. 5.6 Một người chèo thuyền qua một con sông rộng 400 m. Muốn cho thuyền đi theo đường AB, người đó phải luôn hướng mũi thuyền theo hướng AC (Hình 5.1). Biết thuyền qua sông hết 8 min 20 s và vận tốc chảy của dòng nước là 0,6 m/s. Tính vận tốc của thuyền so với dòng nước
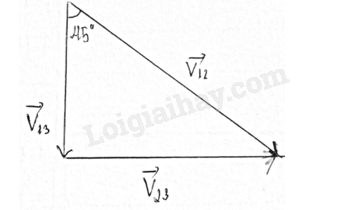
Phương pháp giải: Sử dụng công thức cộng vận tốc được xác định bằng biểu thức: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) Trong đó: + Số 1: gắn với vật cần tính vận tốc + Số 2: gắn với hệ quy chiếu là các vật chuyển động + Số 3: gắn với hệ quy chiếu là các vật đứng yên + v12: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối + v23: vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo + v13: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tuyệt đối. Lời giải chi tiết: Thuyền (1); dòng nước (2); bờ sông (3) Vận tốc của thuyền (1) so với dòng nước (2): \(\overrightarrow {{v_{12}}} \) Vận tốc của dòng nước (2) so với bờ (3): \(\overrightarrow {{v_{23}}} \) Vận tốc của thuyền (1) so với bờ (3): \(\overrightarrow {{v_{13}}} \) AB = 400 m; t = 8 min 20 s = 500s Sử dụng công thức cộng vận tốc được xác định bằng biểu thức: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) Khi đó có độ lớn: = + Có v23 = 0,6 m/s; v13 = \(\frac{{AB}}{t}\) = \(\frac{{400}}{{500}}\) = 0,8 m/s => v12 = 1 m/s Vậy vận tốc của thuyền so với dòng nước là 1 m/s. 5.7 Một ô tô đang chạy với vận tốc v theo phương nằm ngang thì người ngồi trong xe trông thấy giọt mưa rơi tạo thành những vạch làm với phương thẳng đứng một góc 45°. Biết vận tốc rơi của các giọt nước mưa so với mặt đất là 5 m/s. Tính vận tốc của ô tô. Phương pháp giải: Sử dụng công thức cộng vận tốc được xác định bằng biểu thức: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) Trong đó: + Số 1: gắn với vật cần tính vận tốc + Số 2: gắn với hệ quy chiếu là các vật chuyển động + Số 3: gắn với hệ quy chiếu là các vật đứng yên + v12: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối + v23: vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo + v13: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tuyệt đối. Lời giải chi tiết: Gọi (1) là giọt nước mưa, (2) là ô tô, (3) là mặt đường. Vận tốc của giọt nước mưa (1) so với ô tô (2): \(\overrightarrow {{v_{12}}} \) Vận tốc của ô tô (2) so với mặt đường (3): \(\overrightarrow {{v_{23}}} \) Vận tốc của giọt nước mưa (1) so với mặt đường (3): \(\overrightarrow {{v_{13}}} \) Ta có sơ đồ vận tốc như sau:
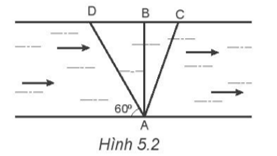
Vì giọt mưa rơi tạo thành những vạch làm với phương thẳng đứng một góc 45° và giọt nước mưa chuyển động rơi thẳng đứng so với mặt đường. Ta có: tan 45o = \(\frac{{{v_{23}}}}{{{v_{13}}}}\). Với v13 là vận tốc của giọt nước mưa so với mặt đất: v13 = 5 m/s. v23 là vận tốc của ô tô so với đường. => v23 = tan 45o x 5 = 5 m/s. Vậy vận tốc của ô tô là 5 m/s. 5.8 Một ca nô chạy ngang qua một dòng sông, xuất phát từ A, hướng mũi về B. Sau 100 s, ca nô cập bờ bên kia ở điểm C cách B 200 m. Nếu người lái hướng mũi ca nô theo hướng AD và vẫn giữ tốc độ máy như cũ thì ca nô sẽ cập bờ bên A kia tại đúng điểm B. Tìm: a) Vận tốc của dòng nước so với bờ sông. b) Vận tốc của ca nô so với dòng nước. c) Chiều rộng của sông.
Phương pháp giải: Sử dụng công thức cộng vận tốc được xác định bằng biểu thức: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) Trong đó: + Số 1: gắn với vật cần tính vận tốc + Số 2: gắn với hệ quy chiếu là các vật chuyển động + Số 3: gắn với hệ quy chiếu là các vật đứng yên + v12: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối + v23: vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo + v13: vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tuyệt đối. Lời giải chi tiết: ∆t = 100 s; BC = 200 m a) Gọi ca nô (1); dòng nước (2); bờ sông (3) Vận tốc của ca nô (1) so với dòng nước (2): \(\overrightarrow {{v_{12}}} \) Vận tốc của dòng nước (2) so với bờ (3): \(\overrightarrow {{v_{23}}} \) Vận tốc của ca nô (1) so với bờ (3): \(\overrightarrow {{v_{13}}} \) Khi mũi ca nô hướng về B thì ta có sơ đồ các vectơ vận tốc như sau:
\(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) Khi đó: v23 = \(\frac{{BC}}{{\Delta t}}\)= \(\frac{{200}}{{100}}\)= 2 m/s. Vận tốc của dòng nước so với bờ sông là 2 m/s. b) Khi mũi ca nô hướng về D ta có sơ đồ các vectơ vận tốc như sau:
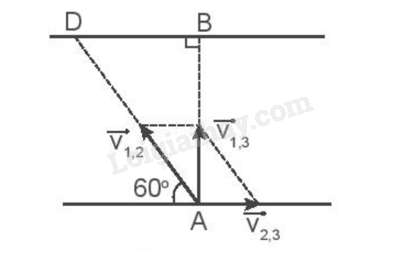
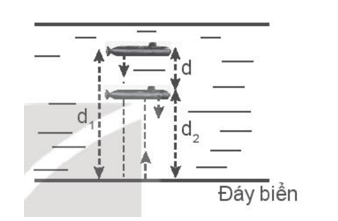
\(\overrightarrow {v{'_{13}}} = \overrightarrow {v{'_{12}}} + \overrightarrow {v{'_{23}}} \) Với v’23 = v23 = 2 m/s(vận tốc của dòng nước là không đổi) v’12 = v12 (vận tốc của ca nô không đổi) Vì v12 là cạnh huyền của tam giác vuông có một góc là 30o nên ta có: v12 = \(\frac{{{v_{23}}}}{{\sin {{30}^o}}}\)= 2v23 = 2.2 = 4 m/s. Vậy vận tốc của ca nô so với dòng nước là 4 m/s. c) Ta có v12 = \(\frac{{AB}}{{\Delta t}}\)= 4 m/s => AB = 4 x 100 = 400 m. 5.9 Một tàu ngầm đang lặn xuống theo phương thẳng đứng với vận tốc không đổi v. Máy sonar định vị của tàu phát tín hiệu siêu âm theo phương thẳng đứng xuống đáy biển. Biết thời gian tín hiệu đi từ tàu xuống đáy biển là t1, thời gian tín hiệu phản hồi từ đáy biển tới tàu là t2, vận tốc của siêu âm trong nước biển là u và đáy biển nằm ngang. Tính vận tốc lặn y của tàu theo u, t1, t2. Phương pháp giải: Tính độ dịch chuyển của tàu ngầm khi phát tín hiệu đến khi nhận được tín hiệu (t1 + t2). Tính độ dịch chuyển của tín hiệu âm khi được phát ra từ tàu đến đáy biển (t1) và từ đáy biển đến khi tàu nhận được tín hiệu phản hồi (t2). Sử dụng công thức d = v.∆t Rút v theo u, t1, t2. Lời giải chi tiết:
Trong thời gian (t1 + t2), con tàu đã lặn sâu được một đoạn d = v(t1 + t2) ⇨ v = \(\frac{d}{{{t_1} + {t_2}}}\) (1) Trong thời gian t1, tín hiệu phát truyền được một đoạn d1 = ut1. Trong thời gian t2, tín hiệu phát truyền được một đoạn d2 = ut2. Vì d = d1 – d2 = u(t1 – t2) (2) Từ (1), (2) => v = \(u\frac{{{t_1} - {t_2}}}{{{t_1} + {t_2}}}\).
|