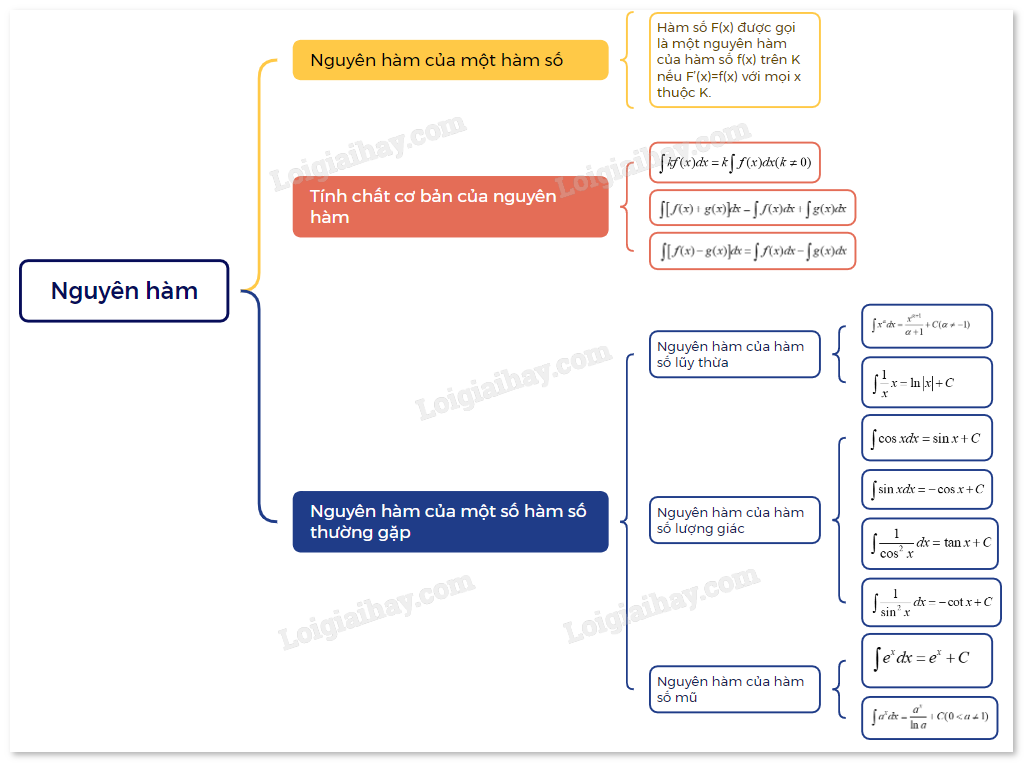
Lý thuyết Nguyên hàm Toán 12 Chân trời sáng tạo1. Khái niệm nguyên hàm 1. Khái niệm nguyên hàm
Chú ý: Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó: a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K. b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K. Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + C là họ các nguyên hàm của f(x) trên K, kí hiệu bởi \(\int {f(x)dx} \) và viết \(\int {f(x)dx} = F(x) + C\). 2. Nguyên hàm của một số hàm sơ cấp a) Nguyên hàm của hàm số lũy thừa
b) Nguyên hàm của hàm số \(y = \frac{1}{x}\)
c) Nguyên hàm của một số hàm số lượng giác
d) Nguyên hàm của hàm số mũ
3. Tính chất cơ bản của nguyên hàm
|