Lý thuyết Phương trình bậc hai một ẩn Toán 9 Kết nối tri thức1. Định nghĩa phương trình bậc hai một ẩn Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng \(a{x^2} + bx + c = 0\), trong đó x là ẩn; a, b, c là những số cho trước gọi là hệ số và \(a \ne 0\). 1. Định nghĩa phương trình bậc hai một ẩn
Ví dụ: Phương trình \(2{x^2} - 3x + 1 = 0\) là phương trình bậc hai với \(a = 2;b = - 3;c = 1\). Phương trình \({x^2} - 3 = 0\) là phương trình bậc hai với \(a = 1,b = 0,c = - 3\). Phương trình \(0{x^2} - 2x - 3 = 0\) không là phương trình bậc hai vì \(a = 0\). 2. Cách giải phương trình bậc hai một ẩn có dạng đặc biệt Giải phương trình bậc hai khuyết số hạng tự do (dạng \(a{x^2} + bx = 0\) \(\left( {a \ne 0,c = 0} \right)\))
Ví dụ: Giải phương trình \(2{x^2} - 4x = 0\) Ta có: \(\begin{array}{l}2{x^2} - 4x = 0\\2x\left( {x - 2} \right) = 0\end{array}\) \(x = 0\) hoặc \(x - 2 = 0\) \(x = 0\) hoặc \(x = 2\). Vậy phương trình có hai nghiệm \({x_1} = 0,{x_2} = 2\). Giải phương trình bậc hai khuyết số hạng bậc nhất (dạng \(a{x^2} + c = 0\) \(\left( {a \ne 0,b = 0} \right)\))
Ví dụ: 1. Giải phương trình \({x^2} - 9 = 0\) Ta có: \(\begin{array}{l}{x^2} - 9 = 0\\{x^2} = 9\end{array}\) \(x = 3\) hoặc \(x = - 3\) Vậy phương trình có hai nghiệm \({x_1} = 3,{x_2} = - 3\). 2. Giải phương trình \({\left( {x + 1} \right)^2} = 3\) Ta có: \({\left( {x + 1} \right)^2} = 3\) \(x + 1 = \sqrt 3 \) hoặc \(x + 1 = - \sqrt 3 \) \(x = - 1 + \sqrt 3 \) hoặc \(x = - 1 - \sqrt 3 \) Vậy phương trình có hai nghiệm \({x_1} = - 1 + \sqrt 3 ,{x_2} = - 1 - \sqrt 3 \). Giải phương trình bậc hai dạng \({x^2} + bx = c\)
Ví dụ: Giải phương trình \({x^2} - 4x = 1\) Ta có: \(\begin{array}{l}{x^2} - 4x = 5\\{x^2} - 4x + 4 = 5 + 4\\{\left( {x - 2} \right)^2} = 9\end{array}\) \(x - 2 = 3\) hoặc \(x - 2 = - 3\) suy ra \(x = 5\) hoặc \(x = - 1\). Vậy phương trình có hai nghiệm \({x_1} = 5,{x_2} = - 1\). 3. Công thức nghiệm của phương trình bậc hai Công thức nghiệm của phương trình bậc hai:
Ví dụ: Giải phương trình \({x^2} - 7x - 8 = 0\). Ta có: \(a = 1,b = - 7,c = - 8\). \(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.1.\left( { - 8} \right) = 81 > 0\). Vậy phương trình có hai nghiệm phân biệt là \({x_1} = \frac{{ - \left( { - 7} \right) + \sqrt {81} }}{{2.1}} = 8;{x_2} = \frac{{ - \left( { - 7} \right) - \sqrt {81} }}{{2.1}} = - 1\). Chú ý: Nếu phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có a và c trái dấu, tức là \(ac < 0\), thì \(\Delta = {b^2} - 4ac > 0\). Khi đó, phương trình có hai nghiệm phân biệt. Ví dụ: Phương trình \({x^2} + 3572x - 3573 = 0\) có \(a = 1 > 0,c = - 3573 < 0\), suy ra a và c trái dấu. Do đó phương trình có hai nghiệm phân biệt. Công thức nghiệm thu gọn của phương trình bậc hai:
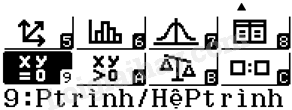
Ví dụ: Giải phương trình \(7{x^2} - 12x + 5 = 0\). Ta có: \(a = 7,b' = - 6,c = 5\). \(\Delta ' = b{'^2} - ac = {\left( { - 6} \right)^2} - 7.5 = 1 > 0\). Vậy phương trình có hai nghiệm phân biệt là \({x_1} = \frac{{ - \left( { - 6} \right) + 1}}{7} = 1;{x_2} = \frac{{ - \left( { - 6} \right) - 1}}{7} = \frac{5}{7}\). 3. Tìm nghiệm của phương trình bậc hai bằng máy tính cầm tay Sử dụng máy tính cầm tay, ta có thể dễ dạng tìm nghiệm của các phương trình bậc hai. Bước 1. Ta sử dụng loại máy tính cầm tay (MTCT) có chức năng này (có phím MODE/MENU). Đối với máy Fx-570VN PLUS, ta bấm phím MODE rồi bấm phím 5 rồi bấm phím 3 để chuyển về chế độ giải phương trình bậc hai. Đối với máy Fx-580VNX, ta bấm MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).
Bấm phím 2 để chọn Polynomial Degree
Cuối cùng, bấm phím 2 để giải phương trình bậc hai
Bước 2. Ta nhập các hệ số \(a,b,c\) bằng cách bấm
Đối với phương trình bậc hai có nghiệm kép, ta nhận được kết quả hiển thị trên màn hình như sau:
Đối với phương trình bậc hai vô nghiệm, ta nhận được kết quả hiển thị trên màn hình như sau:
|