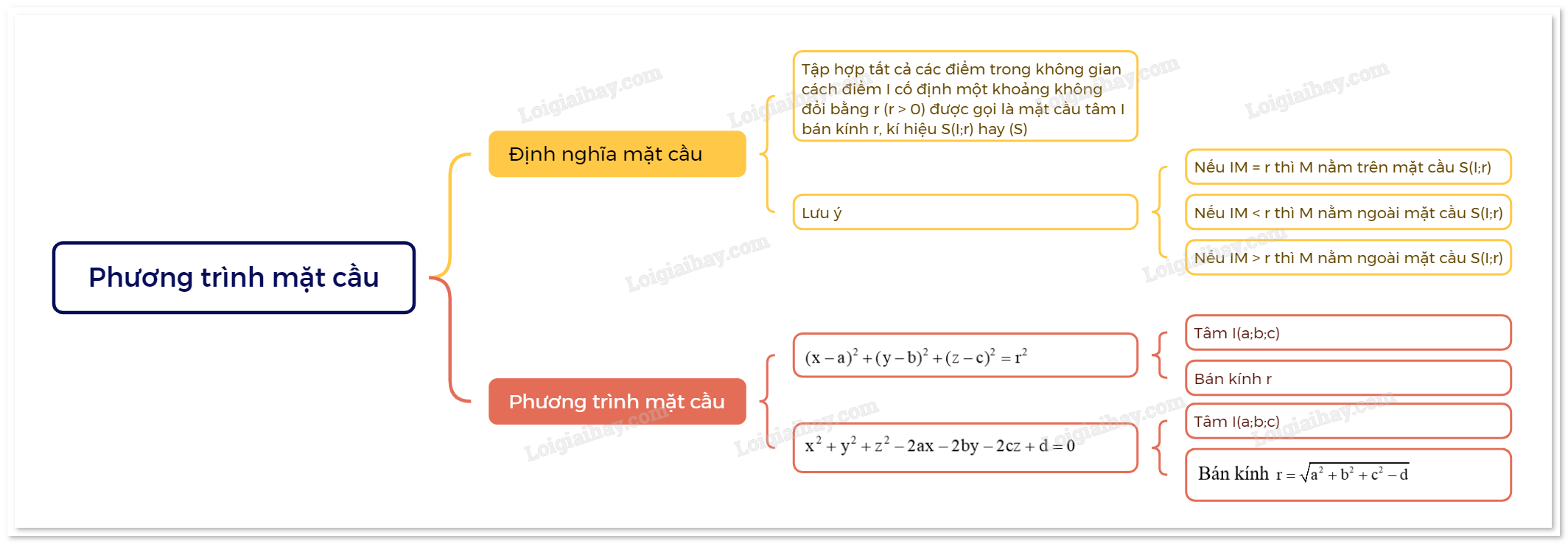
Lý thuyết Phương trình mặt cầu Toán 12 Cùng khám phá

1. Định nghĩa mặt cầu

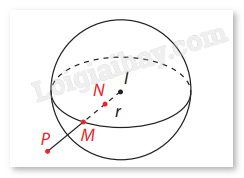
Lưu ý: Cho mặt cầu S(I;r) và điểm M bất kì trong không gian.

- Nếu IM = r thì M nằm trên mặt cầu S(I;r).

- Nếu IM < r thì M nằm ngoài mặt cầu S(I;r).

- Nếu IM > r thì M nằm ngoài mặt cầu S(I;r).

Ví dụ:

- Điểm M nằm trên mặt cầu (S).
- Điểm N nằm trong mặt cầu (S).
- Điểm P nằm ngoài mặt cầu (S).

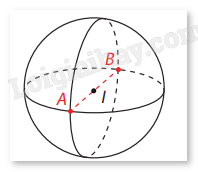
- Nếu hai điểm A, B nằm trên mặt cầu S(I;r) và đoạn thẳng AB đi qua tâm I thì AB được gọi là một đường kính của mặt cầu. Khi đó độ dài đường kính bằng 2r.
- Một mặt cầu được xác định khi ta biết tâm và bán kính hoặc biết một đường kính của nó.

Ví dụ: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu tâm I(-2;1;5) bán kính 3. Các điểm A(10;1;2), B(0;1;4), C(0;3;4) nằm trong, nằm trên hay nằm ngoài mặt cầu đó?

Giải:

Do $IA = \sqrt {{{\left( {10 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {2 - 5} \right)}^2}}  = \sqrt {153}  > 3$ nên điểm A(10;1;2) nằm ngoài mặt cầu đó.

Do $IB = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}}  = \sqrt 5  < 3$ nên điểm B(0;1;4) nằm trong mặt cầu đó.

Do $IC = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {3 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}}  = \sqrt 9  = 3$ nên điểm C(0;3;4) nằm trên mặt cầu đó.

2. Phương trình mặt cầu

Ví dụ 1: Trong không gian Oxyz, xác định tâm I và bán kính r của mặt cầu có phương trình:

a) ${(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 16$.

b) ${(x + 2)^2} + {y^2} + {(z + 3)^2} = 4$.

Giải:

a) Ta có ${(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 16 \Leftrightarrow {(x - 1)^2} + {(y - ( - 2))^2} + {(z - 3)^2} = {4^2}$.

Vậy đây là phương trình mặt cầu có tâm I(1;-2;3) và bán kính r = 4.

b) Ta có ${(x + 2)^2} + {y^2} + {(z + 3)^2} = 4 \Leftrightarrow {(x - ( - 2))^2} + {(y - 0)^2} + {(z - ( - 3))^2} = {2^2}$.

Vậy đây là phương trình mặt cầu có tâm I(-2;0;-3) và bán kính r = 2.

Ví dụ 2: Viết phương trình mặt cầu, biết:

a) Có tâm I(1;2;3), bán kính R = 10.

b) Có tâm I(3;-1;-5) và đi qua điểm B(0;2;1).

Giải:

a) Phương trình của mặt cầu tâm I(1;2;3) bán kính R = 10 là ${(x - 1)^2} + {(y - 2)^2} + {(z - 3)^3} = 100$.

b) Bán kính mặt cầu là $R = IB = \sqrt {{{(0 - 3)}^2} + {{(2 + 1)}^2} + {{(1 + 5)}^2}}  = \sqrt {54}$.

Phương trình mặt cầu tâm I(3;-1;-5) bán kính $R = \sqrt {54}$ là ${(x - 3)^2} + {(y + 1)^2} + {(z + 5)^3} = 54$.

Nhận xét:

Cho mặt cầu tâm I(a;b;c) bán kính r có phương trình ${(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}$. Ta có thể viết phương trình đó dưới dạng ${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$, với $d = {a^2} + {b^2} + {c^2} - {R^2}$.

Dạng phương trình ${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$ xác định một mặt cầu khi và chỉ khi ${a^2} + {b^2} + {c^2} - d > 0$ với tâm I(a;b;c) và bán kính $r = \sqrt {{a^2} + {b^2} + {c^2} - d}$.

Ví dụ 3: Mỗi phương tình sau có là phương trình mặt cầu hay không? Vì sao?

a) $2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0$.

b) ${x^2} + {y^2} - 2x + 6y - 8z - 3 = 0$.

Giải:

a) Phương trình $2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0$ không phải phương trình mặt cầu vì hệ số của ${x^2}$ và ${y^2}$ khác nhau.

b) Phương trình ${x^2} + {y^2} - 2x + 6y - 8z - 3 = 0$ không phải phương trình mặt cầu vì không có biểu thức ${z^2}$.

Ví dụ 4: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt cầu đó.

a) ${x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0$.

b) ${x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0$.

Giải:

a) Phương trình ${x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0$ có dạng ${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$ với $a = 2;b =  - 5;c = 1;d = 14$.

Ta có ${a^2} + {b^2} + {c^2} - d = 4 + 25 + 1 - 14 = 16 > 0$.

Suy ra phương trình đã cho là phương trình mặt cầu tâm I(2;-5;1), bán kính R = 4.

b) Phương trình ${x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0$ có dạng ${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$ với $a =  - 1;b =  - 2;c = 3;d = 20$.

Ta có ${a^2} + {b^2} + {c^2} - d = 1 + 4 + 9 - 20 =  - 6 < 0$.

Suy ra phương trình đã cho không phải phương trình mặt cầu.