Lý thuyết Tích vô hướng của hai vecto - SGK Toán 10 Cánh diều

I. ĐỊNH NGHĨA II. TÍCH CHẤT III. MỘT SỐ ỨNG DỤNG

A. Lý thuyết

1. Định nghĩa

a) Tích vô hướng của hai vecto có cùng điểm đầu

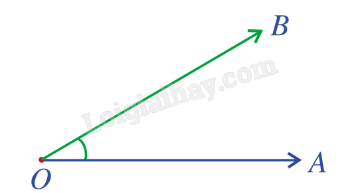
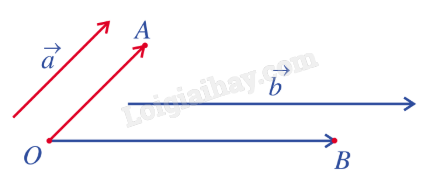
Góc giữa hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) là góc giữa hai tia OA, OB và được kí hiệu là \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\).

Tích vô hướng của hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) là một số thực, kí hiệu \(\overrightarrow {OA} .\overrightarrow {OB} \), được xác định bởi công thức: \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\).

b) Tích vô hướng của hai vecto tùy ý

Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\). Lấy một điểm O và vẽ vecto \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \).

Góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\), là góc giữa hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \).

Tích vô hướng của hai vecto \(\overrightarrow a ,\overrightarrow b \), kí hiệu \(\overrightarrow a .\overrightarrow b \), là tích vô hướng của hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \). Như vậy, tích vô hướng của hai vecto \(\overrightarrow a ,\overrightarrow b \) là một số thực được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).

Quy ước: Tích vô hướng của một vecto bất kì vói vecto \(\overrightarrow 0 \) là số 0.

Chú ý:

+) \(\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right)\).

+) Nếu \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^o}\) thì ta nói hai vecto \(\overrightarrow a ,\overrightarrow b \) vuông góc với nhau, kí hiệu \(\vec a \bot \vec b\) hoặc \(\overrightarrow a \bot \overrightarrow b \). Khi đó \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos {90^o} = 0\).

+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.

+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.

2. Tính chất

Với hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \) và số thực k tùy ý, ta có:

+) \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a \) (tính chất giao hoán).

+) \(\overrightarrow a .\left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c \) (tính chất phân phối).

+) \(\left( {k\overrightarrow a } \right).\overrightarrow b = k\left( {\overrightarrow a .\overrightarrow b } \right) = \overrightarrow a .\left( {k\overrightarrow b } \right)\).

+) \({\overrightarrow a ^2} \ge 0\), \({\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0 \).

Trong đó, kí hiệu \(\overrightarrow a .\overrightarrow a = {\overrightarrow a ^2}\) và biểu thức này được gọi là bình phương vô hướng của vecto \(\overrightarrow a \).

3. Một số ứng dụng

a) Tính độ dài của đoạn thẳng

Nhận xét: Với hai điểm A, B phân biệt, ta có \({\overrightarrow {AB} ^2} = {\left| {\overrightarrow {AB} } \right|^2}\). Do đó, độ dài đoạn thẳng AB được tính như sau: \(AB = \sqrt {{{\overrightarrow {AB} }^2}} \).

b) Chứng minh hai đường thẳng vuông góc

Nhận xét: Cho hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \). Ta có: \(\overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \overrightarrow a \bot \overrightarrow b \).

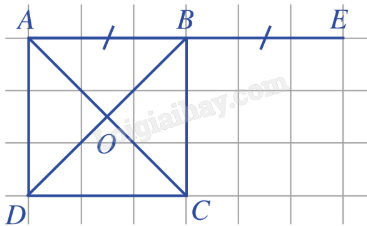
B. Bài tập

Bài 1: Cho tam giác ABC vuông cân tại A và AB = 4 cm.

a) Tính độ dài cạnh huyền BC.

b) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \); \(\overrightarrow {BA} .\overrightarrow {BC} \).

Giải:

a) \(BC = AB\sqrt 2 = 4\sqrt 2 \) (cm).

b) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)

\( = 4.4.\cos \widehat {BAC} = 16.\cos {90^o} = 16.0 = 0\).

\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\)

\( = 4.4\sqrt 2 .\cos \widehat {ABC} = 16\sqrt 2 .\cos {45^o} = 16\sqrt 2 .\frac{{\sqrt 2 }}{2} = 16\).

Bài 2: Cho hình vuông ABCD tâm O có độ dài cạnh bằng a. Tính:

a) \(\overrightarrow {AB} .\overrightarrow {OC} \).

b) \(\overrightarrow {AB} .\overrightarrow {BD} \).

c) \(\overrightarrow {AB} .\overrightarrow {OD} \).

Giải:

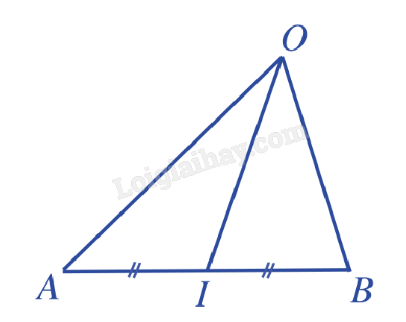
a) Ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {OC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) = \widehat {BAO} = {45^o}\).

Vậy \(\overrightarrow {AB} .\overrightarrow {OC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {OC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {OC} } \right) = a.\frac{a}{{\sqrt 2 }}.\cos {45^o} = \frac{{{a^2}}}{{\sqrt 2 }}.\frac{{\sqrt 2 }}{2} = \frac{{{a^2}}}{2}\).

b) Vẽ vecto \(\overrightarrow {BE} = \overrightarrow {AB} \). Ta có:

\(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {BE} ,\overrightarrow {BD} } \right) = \widehat {EBD} = {135^o}\).

Vậy \(\overrightarrow {AB} .\overrightarrow {BD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BD} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = a.a\sqrt 2 .\cos {135^o} = {a^2}\sqrt 2 .\frac{{ - \sqrt 2 }}{2} = - {a^2}\).

c) Vì \(\overrightarrow {BE} = \overrightarrow {AB} \), \(\overrightarrow {BO} = \overrightarrow {OD} \) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {OD} } \right) = \left( {\overrightarrow {BE} ,\overrightarrow {BO} } \right) = \widehat {EBO} = {135^o}\).

Vậy \(\overrightarrow {AB} .\overrightarrow {OD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {OD} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {OD} } \right) = a.\frac{a}{{\sqrt 2 }}.\cos {135^o} = \frac{{{a^2}}}{{\sqrt 2 }}.\frac{{ - \sqrt 2 }}{2} = \frac{{ - {a^2}}}{2}\).

Bài 3: Cho đoạn thẳng AB và I là trung điểm của AB. Chứng minh rằng với mỗi điểm O, ta có:

a) \(\overrightarrow {OI} .\overrightarrow {IA} + \overrightarrow {OI} .\overrightarrow {IB} = 0\).

b) \(\overrightarrow {OI} .\overrightarrow {AB} = \frac{1}{2}\left( {{{\overrightarrow {OB} }^2} - {{\overrightarrow {OA} }^2}} \right)\).

Giải:

a) Vì I là trung điểm của AB nên \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \).

Vậy \(\overrightarrow {OI} .\overrightarrow {IA} + \overrightarrow {OI} .\overrightarrow {IB} = \overrightarrow {OI} .\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) = \overrightarrow {OI} .\overrightarrow 0 = 0\).

b) Vì I là trung điểm AB nên \(2\overrightarrow {OI} = \overrightarrow {OB} + \overrightarrow {OA} \Leftrightarrow \overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OA} } \right)\).

Vậy \(\overrightarrow {OI} .\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OA} } \right).\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right) = \frac{1}{2}.\left( {{{\overrightarrow {OB} }^2} - {{\overrightarrow {OA} }^2}} \right)\).

Bài 4: Cho tam giác ABC vuông tại A. Tính \(\overrightarrow {AB} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {BC} \).

Giải:

\(\overrightarrow {AB} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {AB} .\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) = \overrightarrow {AB} .\overrightarrow {AC} = 0\) (do \(\overrightarrow {AB} \) vuông góc với \(\overrightarrow {AC} \)).

Bài 5: Chứng minh rằng trong tam giác ABC, ta có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A\) (định lí cosin trong tam giác).

Giải:

Ta có \({\overrightarrow {BC} ^2} = {\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)^2} = {\overrightarrow {AC} ^2} + {\overrightarrow {AB} ^2} - 2.\overrightarrow {AC} .\overrightarrow {AB} \).

Suy ra \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)

\( = A{B^2} + A{C^2} - 2AB.AC.\cos A\).