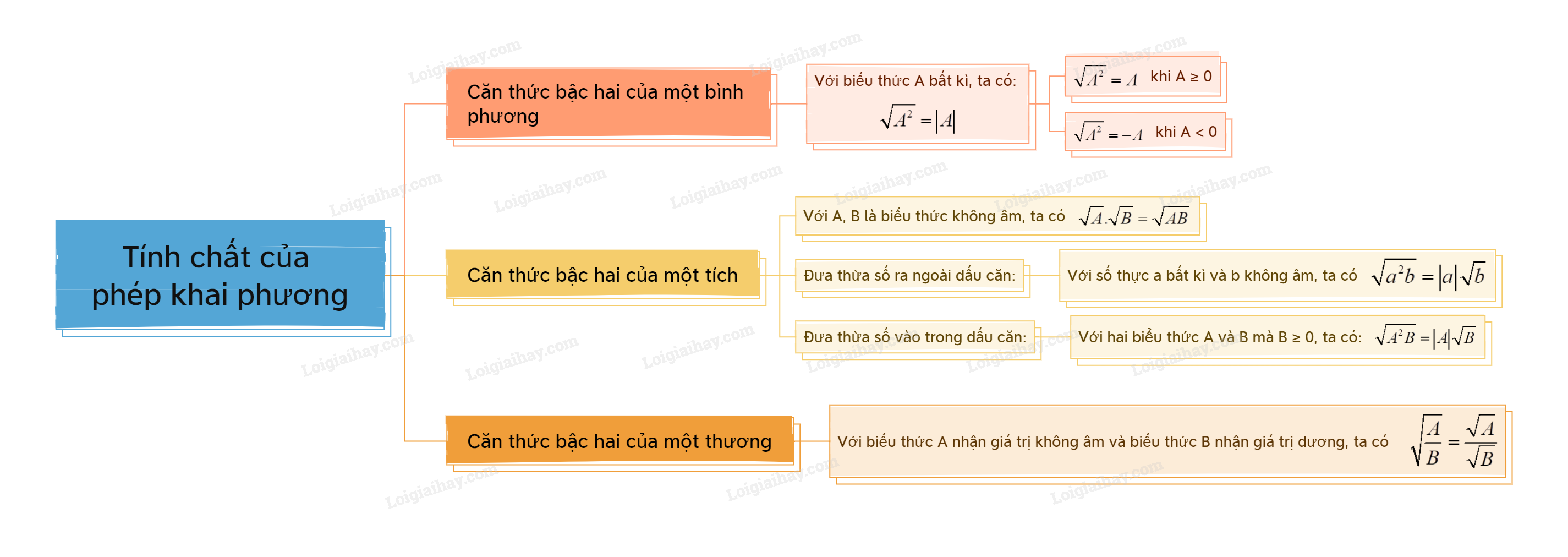
Lý thuyết Tính chất của phép khai phương Toán 9 Chân trời sáng tạo1. Căn thức bậc hai của một bình phương Tính chất Với biểu thức A bất kì, ta có (sqrt {{A^2}} = left| A right|), nghĩa là (sqrt {{A^2}} = A) khi (A ge 0); (sqrt {{A^2}} = - A) khi (A < 0). 1. Căn thức bậc hai của một bình phương Tính chất
Ví dụ: Với \(x < 0\), ta có 1 – x > 0. Do đó \({\left( {\sqrt {1 - x} } \right)^2} = 1 - x\). 2. Căn thức bậc hai của một tích
Ví dụ: \(\sqrt {27} .\sqrt 3 = \sqrt {27.3} = \sqrt {81} = 9\) Với \(a \ge 0,b < 0\) thì \(\sqrt {25{a^2}{b^2}} = \sqrt {{5^2}.{a^2}.{{\left( { - b} \right)}^2}} = \sqrt {{5^2}} .\sqrt {{a^2}} .\sqrt {{{\left( { - b} \right)}^2}} = 5.a.\left( { - b} \right) = - 5ab\). Nhận xét: Ta có thể biến đổi \(\sqrt {ab} = \sqrt a .\sqrt b \) hoặc \(\sqrt a .\sqrt b = \sqrt {ab} \) (\(a \ge 0\) và \(b \ge 0\)) để việc tính toán được dễ dàng hơn.
Tổng quát, với hai biểu thức A và B mà \(B \ge 0\), ta có \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \). Ví dụ: \(\sqrt {75} = \sqrt {25.3} = \sqrt {{5^2}.3} = 5\sqrt 3 \) \(\sqrt {15a} .\sqrt {3a} = \sqrt {15a.3a} = \sqrt {{3^2}{a^2}.5} = \left| {3a} \right|\sqrt 5 \). 2. Căn thức bậc hai của một thương Tính chất
Ví dụ: \(\sqrt {\frac{{49}}{{64}}} = \frac{{\sqrt {49} }}{{\sqrt {64} }} = \frac{7}{8}\); \(\sqrt {\frac{{4{a^2}}}{{25}}} = \frac{{\sqrt {4{a^2}} }}{{\sqrt {25} }} = \frac{{\sqrt 4 .\sqrt {{a^2}} }}{{\sqrt {25} }} = \frac{{2\left| a \right|}}{5}\); \(\frac{{\sqrt 8 }}{{\sqrt 2 }} = \sqrt {\frac{8}{2}} = \sqrt 4 = 2\); Với \(a > 0\) thì \(\frac{{\sqrt {52{a^3}} }}{{\sqrt {13a} }} = \sqrt {\frac{{52{a^3}}}{{13a}}} = \sqrt {4{a^2}} = \sqrt {{{\left( {2a} \right)}^2}} = 2a\). Nhận xét: Ta có thể biến đổi \(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\) hoặc \(\frac{{\sqrt a }}{{\sqrt b }} = \sqrt {\frac{a}{b}} \) (\(a \ge 0\) và \(b > 0\)) để việc tính toán được dễ dàng hơn.
|