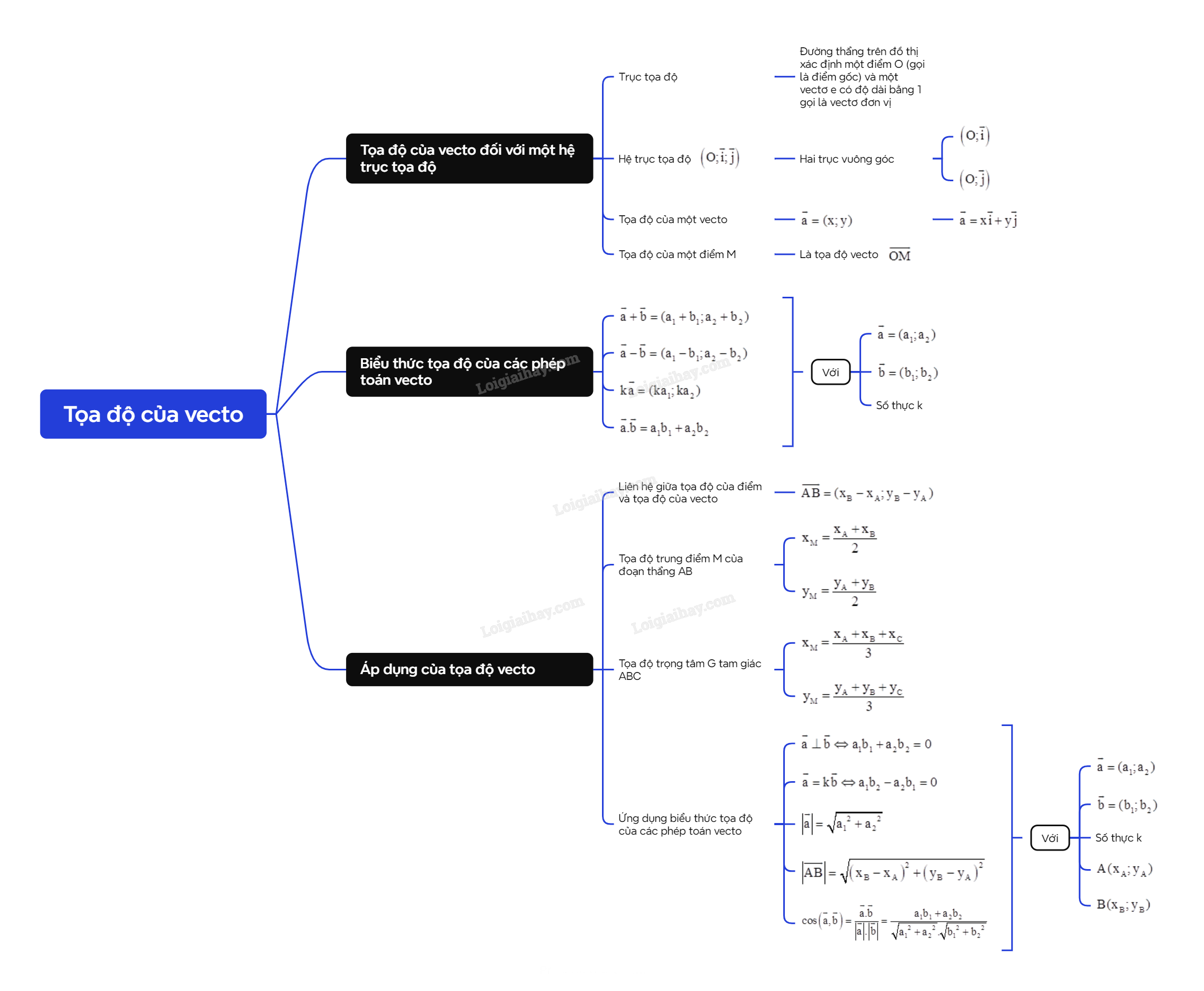
Lý thuyết Tọa độ của vecto - SGK Toán 10 Chân trời sáng tạoA. Lý thuyết 1. Tọa độ của vecto đối với một hệ trục tọa độ a) Trục tọa độ Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đồ thị xác định một điểm O (gọi là điểm gốc) và một vectơ e có độ dài bằng 1 gọi là vectơ đơn vị của trục. A. Lý thuyết 1. Tọa độ của vecto đối với một hệ trục tọa độ a) Trục tọa độ Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đồ thị xác định một điểm O (gọi là điểm gốc) và một vectơ e có độ dài bằng 1 gọi là vectơ đơn vị của trục. Ta ký hiệu trục đó là (O;e).
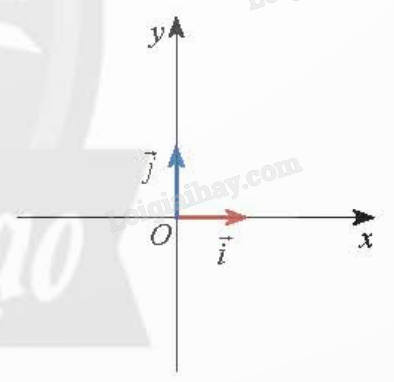
b) Hệ trục tọa độ Hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) gồm hai trục \(\left( {O;\overrightarrow i } \right)\) và \(\left( {O;\overrightarrow j } \right)\) vuông góc với nhau. Điểm góc O chung của hai trục gọi là gốc tọa độ. Trục \(\left( {O;\overrightarrow i } \right)\) được gọi là trục hoành và ký hiệu là Ox, trục \(\left( {O;\overrightarrow j } \right)\) được gọi là trục tung và ký hiệu là Oy. Các vectơ \(\overrightarrow i \) và \(\overrightarrow j \) là các vectơ đơn vị trên Ox và Oy. Hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) còn được ký hiệu là Oxy.
c) Tọa độ của một vecto
Chú ý: + \(\overrightarrow a = (x;y) \Leftrightarrow \overrightarrow a = x\overrightarrow i + y\overrightarrow j \). + Nếu \(\overrightarrow a = ({x_1};{y_1})\) và \(\overrightarrow b = ({x_2};{y_2})\) thì \(\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\). d) Tọa độ của một điểm
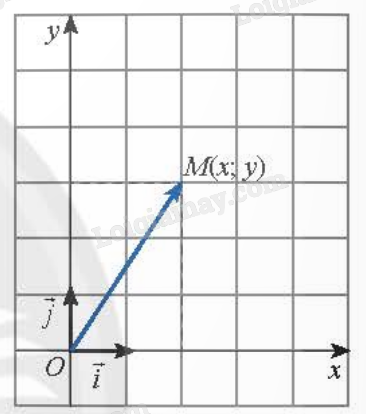
Chú ý: Trong mặt phẳng tọa độ Oxy, ta có: + \(M(x;y) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j \). + Nếu \(\overrightarrow {OM} = (x;y)\) thì x gọi là hoành độ, y gọi là tung độ của điểm M. 2. Biểu thức tọa độ của các phép toán vecto
3. Áp dụng của tọa độ vecto a) Liên hệ giữa tọa độ của điểm và tọa độ của vecto trong mặt phẳng
b) Tọa độ trung điểm của đoạn thẳng và trọng tâm của tam giác
c) Ứng dụng biểu thức tọa độ của các phép toán vecto
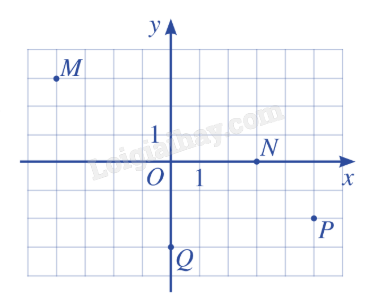
B. Bài tập Bài 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M, N, P, Q. Tìm tọa độ các vecto \(\overrightarrow {OM} \), \(\overrightarrow {ON} \), \(\overrightarrow {OP} \), \(\overrightarrow {OQ} \).
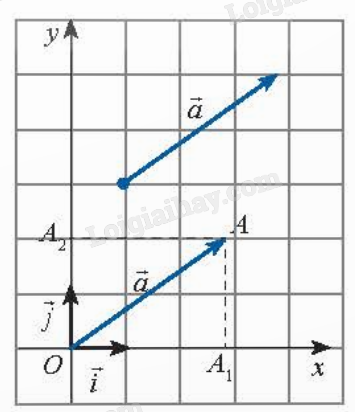
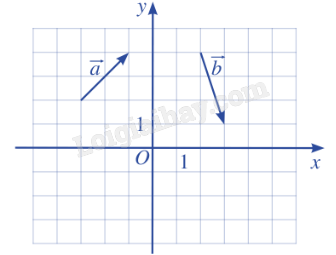
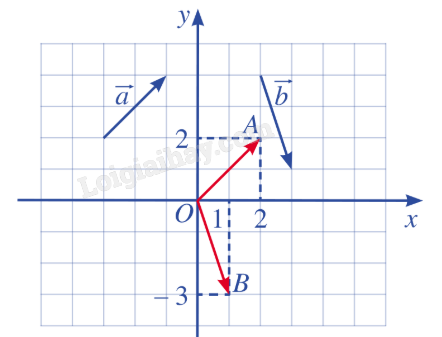
Giải: Từ hình vẽ, ta có: M(-4;3), N(3;0), P(5;-2), Q(0;-3). Do đó: \(\overrightarrow {OM} = ( - 4;3)\), \(\overrightarrow {ON} = (3;0)\), \(\overrightarrow {OP} = (5; - 2)\), \(\overrightarrow {OQ} = (0; - 3)\). Bài 2: Tìm tọa độ của các vecto \(\overrightarrow a \), \(\overrightarrow b \) trong hình.
Giải: Ta có: \(\overrightarrow a = \overrightarrow {OA} \) và A(2;2); tọa độ vecto \(\overrightarrow {OA} \) chính là tọa độ điểm A nên \(\overrightarrow a = (2;2)\). \(\overrightarrow b = \overrightarrow {OB} \) và A(1;-3); tọa độ vecto \(\overrightarrow {OB} \) chính là tọa độ điểm B nên \(\overrightarrow b = (1; - 3)\).
Bài 3: Trong mặt phẳng tọa độ Oxy, cho điểm A(1;2) và vecto \(\overrightarrow u = (3; - 4)\). a) Biểu diễn vecto \(\overrightarrow u \) qua hai vecto \(\overrightarrow i \) và \(\overrightarrow j \). b) Biểu diễn vecto \(\overrightarrow {OA} \) qua hai vecto \(\overrightarrow i \) và \(\overrightarrow j \). Giải: a) Vì \(\overrightarrow u = (3; - 4)\) nên \(\overrightarrow u = 3\overrightarrow i + ( - 4)\overrightarrow j = 3\overrightarrow i - 4\overrightarrow j \). b) Vì điểm A có tọa độ là (1;2) nên \(\overrightarrow {OA} = (1;2)\). Do đó: \(\overrightarrow {OA} = 1\overrightarrow i + 2\overrightarrow j = \overrightarrow i + 2\overrightarrow j \). Bài 4: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(1;1), B(4;3), C(-1;-2). a) Tìm tọa độ của vecto \(\overrightarrow {AB} \). b) Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành. Giải: a) Ta có: \(\overrightarrow {AB} = (4 - 1;3 - 1)\). Vậy \(\overrightarrow {AB} = (3;2)\). b) Gọi tọa độ của điểm D là \(({x_D};{y_D})\), ta có: \(\overrightarrow {DC} = ( - 1 - {x_D}; - 2 - {y_D})\). Tứ giác ABCD là hình bình hành khi và chỉ khi: \(\overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {DC} = (3;2) \Leftrightarrow \left\{ \begin{array}{l} - 1 - {x_D} = 3\\ - 2 - {y_D} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = - 4\\{y_D} = - 4\end{array} \right.\). Vậy D(-4;-4). Bài 5: Cho \(\overrightarrow u = (2; - 1)\), \(\overrightarrow v = (1;5)\). Tìm tọa độ của \(\overrightarrow u + \overrightarrow v \) và \(\overrightarrow u - \overrightarrow v \). Giải: \(\overrightarrow u + \overrightarrow v = (2 + 1; - 1 + 5) = (3;4)\); \(\overrightarrow u - \overrightarrow v = (2 - 1; - 1 - 5) = (1; - 6)\). Bài 6: Cho ba điểm A(-1;-3), B(2;3) và C(3;5). Chứng minh ba điểm A, B, C thẳng hàng. Giải: Ta có: \(\overrightarrow {AB} = (3;6)\), \(\overrightarrow {BC} = (1;2)\). Suy ra \(\overrightarrow {AB} = 3\overrightarrow {BC} \). Vậy ba điểm A, B, C thẳng hàng. Bài 7: Cho tma giác ABC có A(-2;1), B(2;5), C(5;2). Tìm tọa độ trung điểm M của đoạn thẳng AB và trọng tâm G của tam giác ABC. Giải: Do \(M({x_M};{y_M})\) là trung điểm của đoạn thẳng AB nên: \({x_M} = \frac{{ - 2 + 2}}{2} = 0\); \({y_M} = \frac{{1 + 5}}{2} = 3\). Vậy M(0;3). Do \(G({x_G};{y_G})\) là trọng tâm tam giác ABC nên: \({x_G} = \frac{{ - 2 + 2 + 5}}{3} = \frac{5}{3}\); \({y_G} = \frac{{1 + 5 + 2}}{3} = \frac{8}{3}\). Vậy \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\). Bài 8: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;2), B(1;-1), C(8;0). a) Tính \(\overrightarrow {BA} .\overrightarrow {BC} \) và \(\cos \widehat {ABC}\). b) Chứng minh \(\overrightarrow {AB} \bot \overrightarrow {AC} \). c) Giải tam giác ABC. Giải: a) Ta có \(\overrightarrow {BA} = (1;3)\), \(\overrightarrow {BC} = (7;1)\). Do đó \(\overrightarrow {BA} .\overrightarrow {BC} = 1.7 + 3.1 = 10\). Mặt khác: \(\left| {\overrightarrow {BA} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} \), \(\left| {\overrightarrow {BC} } \right| = \sqrt {{7^2} + {1^2}} = \sqrt {50} \). \(\cos \widehat {ABC} = \cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{10}}{{\sqrt {10} .\sqrt {50} }} = \frac{{\sqrt 5 }}{5}\). b) Do \(\overrightarrow {AB} = ( - 1; - 3)\) và \(\overrightarrow {AC} = (6; - 2)\) nên \(\overrightarrow {AB} .\overrightarrow {AC} = ( - 1).6 + ( - 3).( - 2) = 0\). Vậy \(\overrightarrow {AB} \bot \overrightarrow {AC} \). c) Do \(\overrightarrow {AB} \bot \overrightarrow {AC} \) nên \(\widehat {BAC} = {90^o}\), tức tam giác ABC vuông tại A. Mà \(\cos \widehat {ABC} = \frac{{\sqrt 5 }}{5}\) nên \(\widehat {ABC} \approx {63^o}\). Vì thế \(\widehat {ACB} \approx {90^o} - {63^o} = {27^o}\). Mặt khác: \(AB = \left| {\overrightarrow {BA} } \right| = \sqrt {10} \), \(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {50} = 5\sqrt 2 \), \(CA = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{\left( {5\sqrt 2 } \right)}^2} - {{\left( {\sqrt {10} } \right)}^2}} = 2\sqrt {10} \).
|