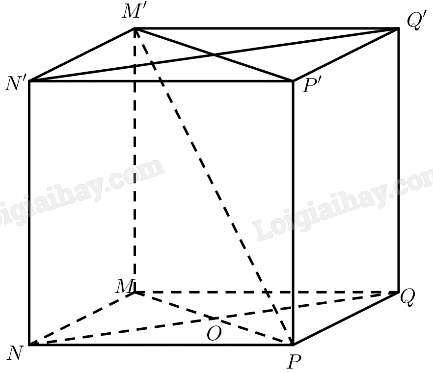
Bài 1 trang 116 SGK Toán 11 tập 2 - Cánh DiềuCho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\). Đề bài Cho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\). a) Góc giữa hai đường thẳng \(MN\) và \(M'P\) bằng: A. \({30^ \circ }\). B. \({45^ \circ }\). C. \({60^ \circ }\). D. \({90^ \circ }\). b) Gọi \(\alpha \) là số đo góc giữa đường thẳng \(M'P\) và mặt phẳng \(\left( {MNPQ} \right)\). Giá trị \(\tan \alpha \) bằng: A. 1. B. 2. C. \(\sqrt 2 \). D. \(\frac{1}{{\sqrt 2 }}\). c) Số đo của góc nhị diện \(\left[ {N,MM',P} \right]\) bằng: A. \({30^ \circ }\). B. \({45^ \circ }\). C. \({60^ \circ }\). D. \({90^ \circ }\). d) Khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {NQQ'N'} \right)\) bằng: A. \(a\). B. \(\frac{a}{{\sqrt 2 }}\). C. \(a\sqrt 2 \). D. \(\frac{a}{2}\). Phương pháp giải - Xem chi tiết a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\) Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\). Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\). Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\). Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\). d) Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng. Lời giải chi tiết
a) \(MM' = PP',MM'\parallel PP'\) \( \Rightarrow MPP'M'\) là hình bình hành \( \Rightarrow MP\parallel M'P' \Rightarrow \left( {MN,M'P'} \right) = \left( {MN,MP} \right) = \widehat {NMP}\) \(MNPQ\) là hình vuông \( \Rightarrow \widehat {NMP} = {45^ \circ }\) Vậy . Chọn B. b) \(MM' \bot \left( {MNPQ} \right) \Rightarrow \left( {M'P,\left( {MNPQ} \right)} \right) = \left( {M'P,MP} \right) = \widehat {MPM'}\) \(MNPQ\) là hình vuông \( \Rightarrow MP = \sqrt {M{N^2} + N{P^2}} = a\sqrt 2 \) \(\tan \widehat {MPM'} = \frac{{MM'}}{{MP}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\) Chọn D. c) \(MM' \bot \left( {MNPQ} \right) \Rightarrow MM' \bot MN,MM' \bot MP\) Vậy \(\widehat {NMP} = {45^ \circ }\) là góc nhị diện \(\left[ {N,MM',P} \right]\). Chọn B. d) Gọi \(O = MP \cap NQ\) \(MNPQ\) là hình vuông \( \Rightarrow MO \bot NQ\) \(NN' \bot \left( {MNPQ} \right) \Rightarrow NN' \bot MO\) \( \Rightarrow d\left( {M,\left( {NQQ'N'} \right)} \right) = MO = \frac{1}{2}MP = \frac{a}{{\sqrt 2 }}\). Chọn B.
|