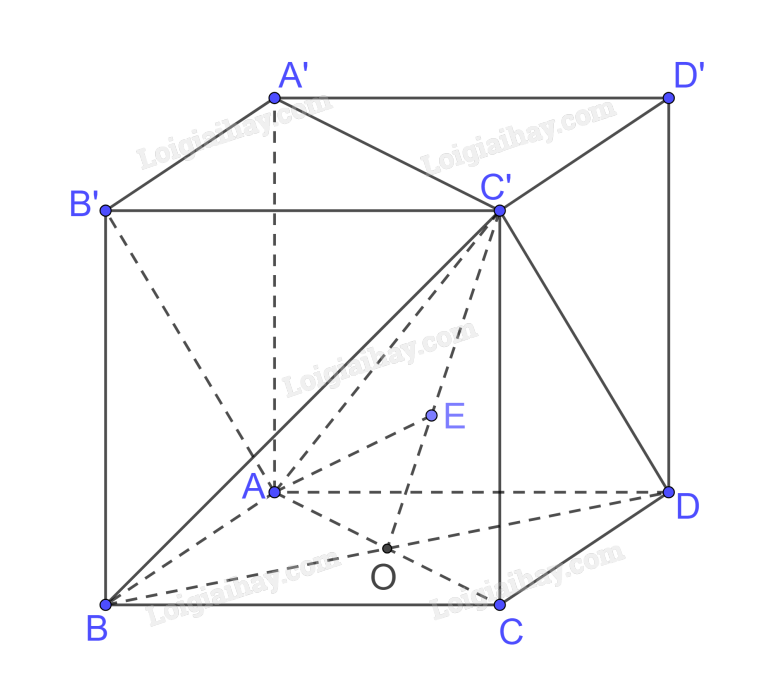
Bài 15 trang 106 SGK Toán 11 tập 2 - Kết nối tri thứcCho hình lập phương (ABCD.A'B'C'D') có (AC' = sqrt 3 ). Khoảng cách giữa hai đường thẳng (AB') và (BC') bằng Đề bài Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AC' = \sqrt 3 \). Khoảng cách giữa hai đường thẳng \(AB'\) và \(BC'\) bằng A. \(\frac{1}{3}\). B. \(\frac{{\sqrt 3 }}{3}\). C. \(\frac{{\sqrt 3 }}{2}\). D. \(\frac{1}{2}\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này đến mặt phẳng song song chứa đường thẳng kia Lời giải chi tiết
Gọi AC giao BD tại O Ta có \(AC \bot BD,BD \bot AA' \Rightarrow BD \bot \left( {ACC'A'} \right);BD \subset \left( {BDC'} \right) \Rightarrow \left( {ACC'A'} \right) \bot \left( {BDC'} \right)\) Mà \(\left( {ACC'A'} \right) \cap \left( {BDC'} \right) = OC'\) Trong (ACCA’) kẻ \(AE \bot OC'\) Do đó \(AE \bot \left( {BDC'} \right)\) Ta có AB’ // DC’ nên \(d\left( {AB',BC'} \right) = d\left( {AB',\left( {BDC'} \right)} \right) = d\left( {A,\left( {BDC'} \right)} \right) = AE\) Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {2A{B^2}} = AB\sqrt 2 \) Xét tam giác ACC’ vuông tại C có \(\begin{array}{l}A{C^2} + C{{C'}^2} = A{{C'}^2}\\ \Leftrightarrow {\left( {AB\sqrt 2 } \right)^2} + A{B^2} = 3\\ \Leftrightarrow 3A{B^2} = 3\\ \Leftrightarrow AB = 1\\ \Leftrightarrow AC = \sqrt 2 \end{array}\) Xét tam giác OCC’ vuông tại C có \(C'O = \sqrt {C{{C'}^2} + O{C^2}} = \sqrt {{1^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = \frac{{\sqrt 6 }}{2}\) Dễ dàng chứng minh \( \Rightarrow \frac{{AE}}{{CC'}} = \frac{{AO}}{{C'O}} \Rightarrow AE = \frac{{AO.CC'}}{{C'O}} = \frac{{\frac{{\sqrt 2 }}{2}.1}}{{\frac{{\sqrt 6 }}{2}}} = \frac{{\sqrt 3 }}{3}\) Đáp án B
|