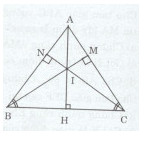
Bài 2 trang 175 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC cân tại A. Kẻ $BM \bot AC(M \in AC),CN \bot AB(N \in AB).$

a) Chứng minh rằng $\Delta BMC = \Delta CNB.$

b) Gọi I là giao điểm của BM với CN. Chứng minh rằng $\Delta AIN = \Delta AIM.$

c) AI cắt BC tại H, biết AB = 10 cm, BC = 12 cm. Tính AH.

Lời giải chi tiết

a)Xét tam giác BMC vuông tại M và CNB vuông tại N có:

BC là cạnh chung.

$\widehat {MCB} = \widehat {NBC}$   (tam giác ABC cân tại A)

Do đó: $\Delta BMC = \Delta CVB$  (cạnh huyền - góc nhọn)

b) Ta có: AN + NB = AB và AM + MC = AC.

Mà AB = AC (tam giác ABC cân tại A)

Nên AN + NB = AM + MC.

Vì BN = MC $(\Delta BMC = \Delta CNB)$

Nên AN = AM.

Xét tam giác ANI vuông tại N và AMI vuông tại M ta có:

AI là cạnh chung.

AN = AM (chứng minh trên)

Do đó: $\Delta ANI = \Delta AMI$  (cạnh huyền - cạnh góc vuông).

c)Xét tam giác ABH và ACH ta có:

AB = AC (tam giác ACB cân tại A)

AH là cạnh chung.

$\widehat {BAH} = \widehat {CAH}(\Delta ANI = \Delta AMI)$

Do đó: $\Delta ABH = \Delta ACH(c.g.c) \Rightarrow BH = CH;\widehat {AHB} = \widehat {AHC}$

Do đó: $BH = CH = {{BC} \over 2} = {{12} \over 2} = 6(cm).$

$\widehat {AHB} + \widehat {AHC} = {180^0}$   (hai góc kề bù)

Nên $\widehat {AHB} + \widehat {AHB} = {180^0}(\widehat {AHB} = \widehat {AHC}) \Rightarrow 2\widehat {AHB} = {180^0} \Rightarrow \widehat {AHB} = {90^0} \Rightarrow AH \bot BC$

Tam giác ABH vuông tại H $\Rightarrow A{H^2} + B{H^2} = A{B^2}$   (định lí Pythagore).

Do đó: $A{H^2} = A{B^2} - B{H^2} = {10^2} - {6^2} = 100 - 36 = 64.$

Mà AH > 0. Vậy $AH = \sqrt {64}  = 8(cm).$

HocTot.XYZ