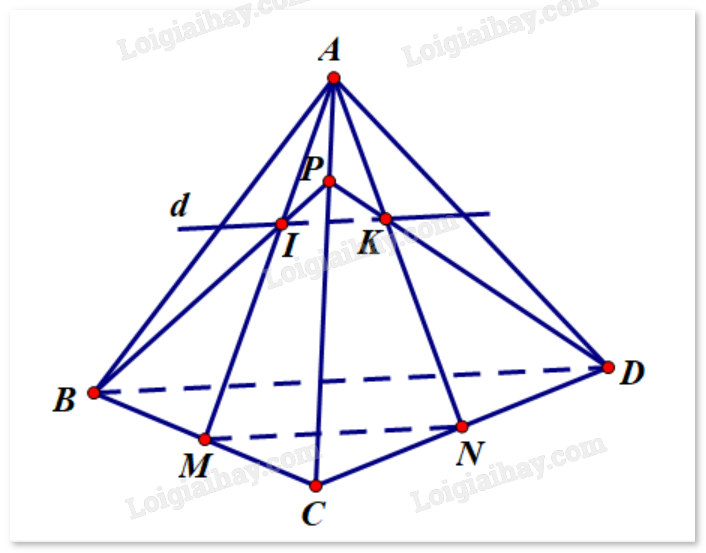
Bài 4.14 trang 82 SGK Toán 11 tập 1 - Kết nối tri thứcCho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC. a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD) b) Chứng minh rằng d song song với BD Đề bài Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC. a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD). b) Chứng minh rằng d song song với BD. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho. Lời giải chi tiết
a) Gọi giao điểm của AM và BP là I, giao điểm của AN và DP là K. Ta có IK đều thuộc mặt phẳng (AMN) và (BPD) suy ra IK là giao tuyến của hai mặt phẳng này. Như vậy, d là đường thẳng đi qua I và K. b) Ta có: \(mp\left( {AMN} \right) \cap mp\left( {BPD} \right) = IK\). \(mp\left( {AMN} \right) \cap mp\left( {BCD} \right) = MN\); \(mp\left( {BPD} \right) \cap mp\left( {BCD} \right) = BD\). Mà MN // BD (do MN là đường trung bình của tam giác BCD) suy ra IK // BD. Như vây, d song song với BD.
|