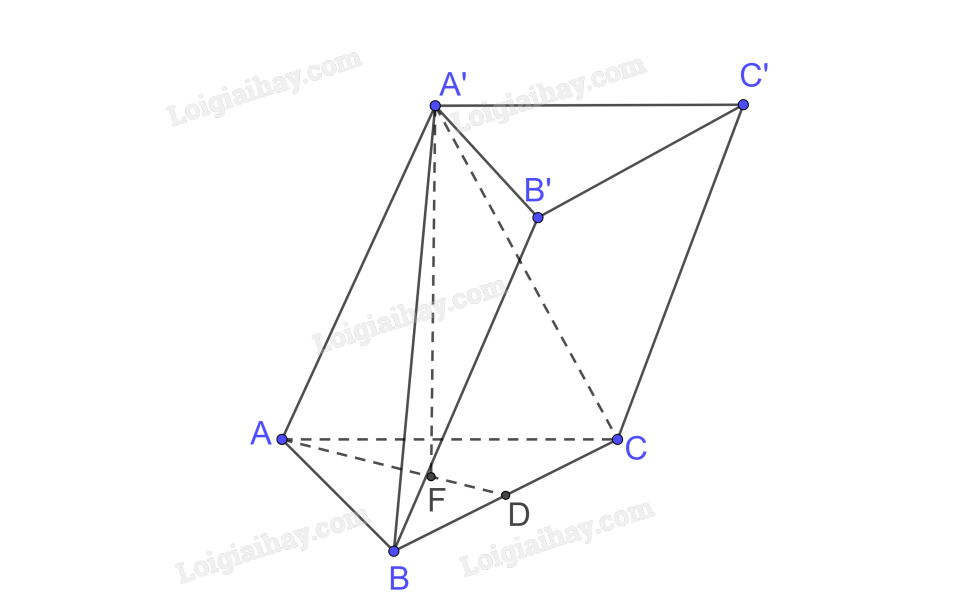
Bài 7.31 trang 63 SGK Toán 11 tập 2 - Kết nối tri thứckhối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a Đề bài Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Thể tích khối lăng trụ \(V = h.S\) Lời giải chi tiết Vì hình chóp A’.ABC có A'A = A'B = A'C và đáy ABC là tam giác đều nên hình chóp A’.ABC đều. Gọi F là hình chiếu của A’ trên (ABC) nên F là tâm của đáy ABC là tam giác đều do đó F cũng là trọng tâm của tam giác ABC. Gọi AF cắt BC tại D Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\) Mà F là trọng tâm nên \(AF = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\) Xét tam giác A’AF vuông tại F có \(A'F = \sqrt {A'{A^2} - A{F^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \) Diện tích tam giác đều ABC là \(S = \frac{{{a^2}\sqrt 3 }}{4}\) Thể tích khối lăng trụ là \(V = A'F.S = \sqrt {{b^2} - \frac{{{a^2}}}{3}} .\frac{{{a^2}\sqrt 3 }}{4}\)
|