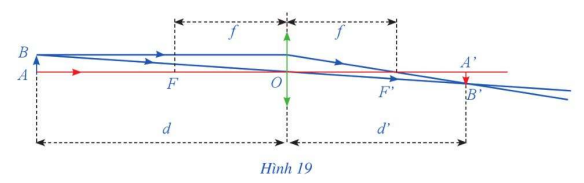
Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh DiềuMột thấu kính hội tụ có tiêu cự là \(f\). Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ một vật thật AB và từ ảnh \(A'B'\) của nó tới quang tâm \(O\) của thấu kính như Hình 19. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\). Đề bài Một thấu kính hội tụ có tiêu cự là \(f\). Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ một vật thật AB và từ ảnh \(A'B'\) của nó tới quang tâm \(O\) của thấu kính như Hình 19. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\). a) Tìm biểu thức xác định hàm số \(d' = \varphi (d)\). b) Tìm \(\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d),\mathop {\lim }\limits_{d \to {f^ - }} \varphi (d)\) và \(\mathop {\lim }\limits_{d \to f} \varphi (d)\). Giải thích ý nghĩa của các kết quả tìm được.
Phương pháp giải - Xem chi tiết Sử dụng công thức \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) Lời giải chi tiết a) Ta có \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \Leftrightarrow \frac{1}{{d'}} = \frac{1}{f} - \frac{1}{d} = \frac{{d - f}}{{df}} \Leftrightarrow d' = \frac{{df}}{{d - f}}\) b) Ta có: \(\left\{ \begin{array}{l}df > 0\\d - f > 0,d \to {f^ + }\end{array} \right.\) \(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \end{array}\) Ta có: \(\left\{ \begin{array}{l}df > 0\\d - f < 0,d \to {f^ - }\end{array} \right.\) Do đó, \(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ - }} \varphi (d) = \mathop {\lim }\limits_{d \to {f^ - }} \frac{{df}}{{d - f}} = - \infty \end{array}\) Vì \(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d)\ne \mathop {\lim }\limits_{d \to {f^ - }} \varphi (d)\end{array}\) Vậy nên không tồn tại \(\begin{array}{l}\mathop {\lim }\limits_{d \to f} \varphi (d) \end{array}\) Giải thích ý nghĩa của các kết quả tìm được: Khi khoảng cách của vật tới thấu kính mà gần với tiêu cự thì khoảng cách ảnh của vật đến thấu kính ra xa vô tận nên lúc đó bằng mắt thường mình không nhìn thấy.
|