Đề thi giữa kì 1 Toán 6 - Đề số 6Tải về Phần trắc nghiệm (4 điểm) Câu 1. Tập hợp A các số tự nhiên lớn hơn 2 và không vượt quá 7 là:
Lựa chọn câu để xem lời giải nhanh hơn
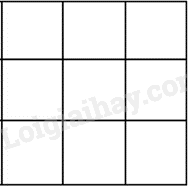
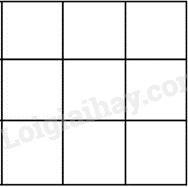
Đề bài Phần trắc nghiệm (4 điểm) Câu 1. Tập hợp A các số tự nhiên lớn hơn 2 và không vượt quá 7 là: A. \(\left\{ {2;3;4;5;6;7} \right\}\) B. \(\left\{ {3;4;5;6} \right\}\) C. \(\left\{ {2;3;4;5;6} \right\}\) D. \(\left\{ {3;4;5;6;7} \right\}\) Câu 2. Kết quả của phép tính \({5^5}{.5^9}\) bằng: A. \({5^{45}}\) . B. \({5^{14}}\) . C. \({25^{14}}\) . D. \({10^{14}}\) . Câu 3. Số 19 được viết trong hệ La Mã là: A. \({\rm{IX}}\) . B. \({\rm{XIV}}\) . C. \({\rm{XIX}}\) . D. \({\rm{IXX}}\) . Câu 4. Luỹ thừa \({3^3}\) có giá trị bằng: A. 6 B. 9 C. 18 D. 27 Câu 5. Các số \(2;19;29\) . Số nào là số nguyên tố A. 2 B. 19 C. 29 D. Cả 3 số trên. Câu 6. Cho tập hợp \({\rm{A}} = {\rm{\{ }}3;x;y;7\} \) ta có: A. \(3 \in {\rm{A}}\) B. \(5 \in {\rm{A}}\) C. \(y \notin {\rm{A}}\) D. \({\rm{\{ }}3;x{\rm{\} }} \in {\rm{A}}\) Câu 7. Số \(24375\) là số A. Chia hết cho 2 và 3 B. Chia hết cho 3 và 5 C. Chia hết cho 2 và 5 D. Chia hết cho 9 Câu 8. Tìm \(x \in \mathbb{N}\) biết \((x - 1).22 = 44\) thì x bằng: A. 12. B. 2. C. 3. D. 66. Câu 9. Số chia hết cho cả \(2;3;5;9\) là: A. \(1825\) B. \(4380\) C. \(4875\) D. \(80820\) Câu 10. Kết quả phép chia \({10^{10}}:{10^5}\) là: A. \({10^2}\) . B. \({10^5}\) . C. \({1^2}\) . D. \({1^5}\) . Câu 11. Xét tập hợp \(\mathbb{N}\) , trong các số sau, bội của 14 là: A. 48 B. 28 C. 36 D. 7 Câu 12. Kết quả phân tích số \(420\) ra thừa số nguyên tố là : A. \({2^2}.3.7\) B. \({2^2}.5.7\) C. \({2^2}.3.5.7\) D. \({2^2}\) Câu 13. Nếu \(m \vdots 5\) và \(n \vdots 5\) thì \(m + n\) chia hết cho: A. 10 B. 25 C. 5 D. 3 Câu 14. Kết quả của phép tính \({3.5^2} - 16:{2^2}\) bằng: A. 71 B. 69 C. 60 D. 26 Câu 15. Số x mà \({2^x}{.2^2} = {2^8}\) là: A. 1 B. 4 C. 6 D. \({2^6}\) Câu 16. Tam giác đều ABC có: A. \(AB = BC = CA\) B. \(AB > BC = CA\) C. \(AB < BC = CA\) D. \(AB < BC < CA\) Câu 17. Cho hình bình hành ABCD có \(AB = 6cm\) ; \(BC = 4cm\) ; \(AH = 2cm\) (AH là đường cao ứng với cạnh CD). Chu vi hình bình hành ABCD là? A. \(10cm\) B. \(20cm\) C. \(24cm\) D. \(12cm\) Câu 18. Hình sau có bao nhiêu hình vuông
A. 13 hình vuông B. 14 hình vuông C. 15 hình vuông D. 16 hình vuông Câu 19. Cho chu vi hình thoi là \(20cm\) . Độ dài cạnh hình thoi là: A. \(2cm\) B. \(5cm\) C. \(10cm\) D. \(4cm\) Câu 20. Một hình chữ nhật có chiều dài là 12m, chiều rộng là 8m. Một hình vuông có chu vi bằng chu vi hình chữ nhật. Diện tích hình vuông đó là : A. \(50{m^2}\) B. \(100{m^2}\) C. \(100c{m^2}\) D. \(50c{m^2}\)
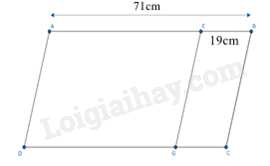
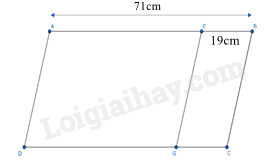
Phần tự luận (6 điểm) Bài 1 (1,5 điểm): Thực hiện các phép tính (tính nhanh nếu có thể) a) \(19.65 + 35.19\) b) \(1024:({2^5}.129 - {2^5}.121)\) c) \({5.3^2} - 32:{4^2}\) Bài 2 (1 điểm): Tìm số tự nhiên x, biết: a) \(100 - 7(x - 5) = 58\) b) \({4.2^x} - 3 = 125\) Bài 3 (1 điểm): a) Viết tập hợp A các số tự nhiên n vừa chia hết cho 2, vừa chia hết cho 5, biết \(32 \le {\rm{n}} \le 62\) b) Thay * bằng chữ số nào để được số \(\overline {607*} \) chia hết cho cả 2 và 3 Bài 4 (1,5 điểm): Một hình bình hành ABCD có \(AB = 71cm\) . Người ta thu hẹp hình bình hành đó thành hình bình hành AEGD có diện tích nhỏ hơn diện tích hình bình hành ban đầu là \(6550{m^2}\) và \(EB = 19cm\) . Tính diện tích hình bình hành ban đầu.
Bài 5 (1,0 điểm): Cho \({\rm{A}} = 1 + 2 + {2^2} + {2^3} + ... + {2^{11}}\) Không tính tổng A, hãy chứng tỏ A chia hết cho 3. - Hết - Lời giải Phần trắc nghiệm
Câu 1. Tập hợp A các số tự nhiên lớn hơn 2 và không vượt quá 7 là:
Phương pháp Liệt kê các số tự nhiên lớn hơn 2 và nhỏ hơn hoặc bằng 7. Lời giải Tập hợp các số tự nhiên lớn hơn 2 và không vượt quá 7 là: \(\left\{ {3;4;5;6;7} \right\}\) . Đáp án D. Câu 2. Kết quả của phép tính \({5^5}{.5^9}\) bằng:
Phương pháp Dựa vào cách nhân lũy thừa cùng cơ số. Lời giải \({5^5}{.5^9} = {5^{5 + 9}} = {5^{14}}\) . Đáp án B. Câu 3. Số 19 được viết trong hệ La Mã là:
Phương pháp Dựa vào cách viết số La Mã. Lời giải Số 19 được viết trong hệ La Mã là: \({\rm{XIX}}\) . Đáp án C. Câu 4. Luỹ thừa \({3^3}\) có giá trị bằng:
Phương pháp Dựa vào cách tính lũy thừa. Lời giải Ta có: \({3^3} = 3.3.3 = 27\) . Đáp án D. Câu 5. Các số \(2;19;29\) . Số nào là số nguyên tố
Phương pháp Dựa vào kiến thức về số nguyên tố. Lời giải Dựa vào bảng số nguyên tố đã học, ta thấy 2; 19; 29 đều là các số nguyên tố. Đáp án D. Câu 6. Cho tập hợp \({\rm{A}} = {\rm{\{ }}3;x;y;7\} \) ta có:
Phương pháp Dựa vào kiến thức về tập hợp. Lời giải \(3 \in {\rm{A}}\) nên A đúng. \(5 \notin {\rm{A}}\) nên B sai. \(y \in {\rm{A}}\) nên C sai. \({\rm{\{ }}3;x{\rm{\} }}\) là tập hợp => không sử dụng “ \( \in \) ” nên D sai. Đáp án A. Câu 7. Số \(24375\) là số
Phương pháp Dựa vào dấu hiệu chia hết. Lời giải Số 24375 có chữ số tận cùng là 5 nên chia hết cho 5 nhưng không chia hết cho 2. Ta có: 2 + 4 + 3 + 7 + 5 = 21 \( \vdots \) 3 nhưng không chia hết cho 9 nên số 24375 chia hết cho 3 nhưng không chia hết cho 9. Vậy số 24375 chia hết cho 3 và 5. Đáp án B. Câu 8. Tìm \(x \in \mathbb{N}\) biết \((x - 1).22 = 44\) thì x bằng:
Phương pháp Sử dụng quy tắc chuyển vế để tìm x. Lời giải \(\begin{array}{l}(x - 1).22 = 44\\x - 1 = 44:22\\x - 1 = 2\\x = 2 + 1\\x = 3\end{array}\) Đáp án C. Câu 9. Số chia hết cho cả \(2;3;5;9\) là:
Phương pháp Dựa vào dấu hiệu chia hết. Lời giải Số chia hết cho cả 2 và 5 có chữ số tận cùng là 0 nên loại đáp án A và C. Số chia hết cho cả 3 và 9 thì phải chia hết cho 9 nên tổng các chữ số của số đó phải chia hết cho 9. Ta có: 4 + 3 + 8 + 0 = 15 không chia hết cho 9. 8 + 0 + 8 + 2 + 0 = 18 chia hết cho 9. Vậy số chia hết cho cả 2; 3; 5; 9 là 80820. Đáp án D.
Câu 10. Kết quả phép chia \({10^{10}}:{10^5}\) là:
Phương pháp Dựa vào quy tắc chia hai lũy thừa cùng cơ số. Lời giải \({10^{10}}:{10^5} = {10^{10 - 5}} = {10^5}\) . Đáp án B. Câu 11. Xét tập hợp \(\mathbb{N}\) , trong các số sau, bội của 14 là:
Phương pháp Dựa vào kiến thức về bội số. Lời giải Ta có: 28 = 14.2 nên 28 là bội của 14. Đáp án B. Câu 12. Kết quả phân tích số \(420\) ra thừa số nguyên tố là :
Phương pháp Dựa vào phân tích một số tự nhiên ra thừa số nguyên tố. Lời giải 420 = 2.2.3.5.7 = 22.3.5.7. Đáp án C. Câu 13. Nếu \(m \vdots 5\) và \(n \vdots 5\) thì \(m + n\) chia hết cho:
Phương pháp Dựa vào dấu hiệu chia hết. Lời giải Nếu \(m \vdots 5\) và \(n \vdots 5\) thì \(m + n\) cũng chia hết cho 5. Đáp án C. Câu 14. Kết quả của phép tính \({3.5^2} - 16:{2^2}\) bằng:
Phương pháp Sử dụng quy tắc tính với số tự nhiên, đưa lũy thừa về số tự nhiên để tính. Lời giải \({3.5^2} - 16:{2^2} = 3.25 - 16:4 = 75 - 4 = 71\) . Đáp án A. Câu 15. Số x mà \({2^x}{.2^2} = {2^8}\) là:
Phương pháp Chuyển vế và thực hiện tính toán với lũy thừa cùng cơ số. Lời giải \(\begin{array}{l}{2^x}{.2^2} = {2^8}\\{2^x} = {2^8}:{2^2}\\{2^x} = {2^{8 - 2}}\\{2^x} = {2^6}\\x = 6\end{array}\) Vậy x = 6. Đáp án C. Câu 16. Tam giác đều ABC có:
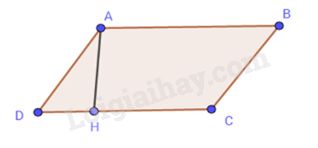
Phương pháp Dựa vào đặc điểm của tam giác đều. Lời giải Trong tam giác đều ba cạnh có độ dài bằng nhau nên AB = BC = CA. Đáp án A. Câu 17. Cho hình bình hành ABCD có \(AB = 6cm\) ; \(BC = 4cm\) ; \(AH = 2cm\) (AH là đường cao ứng với cạnh CD). Chu vi hình bình hành ABCD là ?
Phương pháp Vẽ hình và sử dụng công thức tính chu vi hình bình hành. Lời giải Chu vi hình bình hành ABCD là: C = 2(AB + BC) = 2(6 + 4) = 2.10 = 20 (cm) Đáp án B. Câu 18. Hình sau có bao nhiêu hình vuông
Phương pháp Quan sát hình vẽ. Lời giải Hình trên có 9 hình vuông nhỏ; 4 hình vuông tạo bởi 4 hình vuông nhỏ và 1 hình vuông lớn nên có tổng cộng 9 + 4 + 1 = 14 hình vuông. Đáp án B. Câu 19. Cho chu vi hình thoi là \(20cm\) . Độ dài cạnh hình thoi là :
Phương pháp Dựa vào công thức tính chu vi hình thoi. Lời giải Chu vi của hình thoi là: C = 4.cạnh = 20cm => Độ dài cạnh của hình thoi là 20:4 = 5cm. Đáp án B. Câu 20. Một hình chữ nhật có chiều dài là 12m, chiều rộng là 8m. Một hình vuông có chu vi bằng chu vi hình chữ nhật. Diện tích hình vuông đó là :
Phương pháp Dựa vào công thức tính chu vi và diện tích hình chữ nhật, hình vuông. Lời giải Chu vi hình chữ nhật (hình vuông) là: 2.(12 + 8) = 2.20 = 40(m) Cạnh hình vuông là: 40:4 = 10(m) Diện tích hình vuông đó là: 10.10 = 100 (m2). Đáp án B. Phần tự luận. Bài 1 (1,5 điểm): Thực hiện các phép tính (tính nhanh nếu có thể)
Phương pháp Sử dụng các quy tắc tính với số tự nhiên và lũy thừa. Lời giải a) \(19.65 + 35.19\) \( = 19.\left( {65 + 35} \right)\) \( = 19.100 = 1900\) b) \(1024:({2^5}.129 - {2^5}.121)\) \( = 1024:[{2^5}.(129 - 121)]\) \( = 1024:({2^5}.8)\) \( = {2^{10}}:({2^5}{.2^3})\) \( = {2^{10}}:{2^8} = {2^2}\) c) \({5.3^2} - 32:{4^2}\) \( = 5.9 - 32:16\) \( = 45 - 2 = 43\) Bài 2 (1 điểm): Tìm số tự nhiên x, biết:
Phương pháp Sử dụng quy tắc chuyển vế để tìm x. Lời giải
Bài 3 (1 điểm): a) Viết tập hợp A các số tự nhiên n vừa chia hết cho 2, vừa chia hết cho 5, biết \(32 \le {\rm{n}} \le 62\) b) Thay * bằng chữ số nào để được số \(\overline {607*} \) chia hết cho cả 2 và 3 Phương pháp a) Sử dụng dấu hiệu chia hết cho 2, dấu hiệu chia hết cho 5. b) Sử dụng dấu hiệu chia hết cho 2, dấu hiệu chia hết cho 3. Lời giải a) Các số chia hết cho 2 và 5 thì chữ số tận cùng phải bằng 0, vậy các số n thỏa mãn chữ số tận cùng bằng 0 và \(32 \le {\rm{n}} \le 62\) là: 40; 50; 60. Vậy \(A = \left\{ {40;50;60} \right\}\) . b) Để \(\overline {607*} \) chia hết cho 2. Mà * là chữ số \( \Rightarrow * \in \{ 0;2;4;6;8\} \) (1) Để \(\overline {607*} \) chia hết cho 3 thì \(\left( {6 + 0 + 7 + *} \right)\) chia hết cho 3 hay \(\left( {13 + *} \right)\) chia hết cho 3 (2) Từ (1) và (2) \( \Rightarrow * \in \{ 2;8\} \) Bài 4 (1,5 điểm): Một hình bình hành ABCD có \(AB = 71cm\) . Người ta thu hẹp hình bình hành đó thành hình bình hành AEGD có diện tích nhỏ hơn diện tích hình bình hành ban đầu là \(6550{m^2}\) và \(EB = 19cm\) . Tính diện tích hình bình hành ban đầu. Phương pháp Tính chiều cao của hình bình hành ban đầu. Tính diện tích hình bình hành ABCD. Lời giải Phần diện tích giảm đi khi thu hẹp hình bình hành ABCD thành hình bình hành AEGD chính là diện tích hình bình hành EBCG và bằng \(665c{m^2}\) Chiều cao của hình bình hành EBCG hay ABCD là: \(665:19 = 35\left( {cm} \right)\) Diện tích hình bình hành ABCD là: \(71.35 = 2485(c{m^2})\) Vậy diện tích hình bình hành ABCD là \(2485c{m^2}\) Bài 5 (1,0 điểm): Cho \({\rm{A}} = 1 + 2 + {2^2} + {2^3} + ... + {2^{11}}\) Không tính tổng A, hãy chứng tỏ A chia hết cho 3. Phương pháp Sử dụng cách nhóm nhân tử chung, chứng minh A bằng tích của 3 và một số hạng khác nên A chia hết cho 3. Lời giải Ta có \({\rm{A}} = 1 + 2 + {2^2} + {2^3} + ... + {2^{11}}\) (12 số hạng) A \( = (1 + 2) + ({2^2} + {2^3}) + ... + ({2^{10}} + {2^{11}})\) (6 nhóm) A \( = 3 + {2^2}(1 + 2) + ... + {2^{10}}(1 + 2)\) A \( = 3 + {2^2}.3 + ... + {2^{10}}.3\) A \( = 3.(1 + {2^2} + ... + {2^{10}})\) Vì \(3 \vdots 3\) \( \Rightarrow {\rm{A}} \vdots {\rm{3}}\) (đpcm)
|