Đề thi học kì 1 Toán 6 - Đề số 7Tải vềPhần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
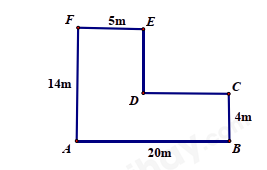
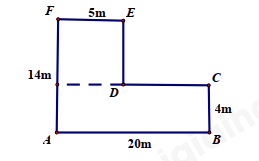
Đề bài Phần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Cho tập hợp \(A = \left\{ {x \in \mathbb{N}|3 < x < 10} \right\}\). Số phần tử của tập hợp A là: A. 5 phần tử B. 6 phần tử C. 7 phần tử D. 8 phần tử Câu 2: Tổng cửa số tự nhiên bé nhất có ba chữ số và số tự nhiên lớn nhất có bốn chữ số là: A. 1999 B. 9100 C. 1099 D. 10 099 Câu 3: Cho hai số nguyên a, b thỏa mãn \(a + b = - 1\). Tích a.b lớn nhất là A. 0 B. 1 C. -2 D. -1 Câu 4: Lũy thừa \({\left( { - 3} \right)^3}\) có giá trị bằng A. 27 B. 9 C. -27 D. -9 Câu 5: Sắp xếp các số nguyên 3; -13; 17; -5; 0 theo thứ tự tăng dần là: A. -5; -13; 0; 3; 17 B. 0; -13; -5; 3; 17 C. 17; 3; 0; -5; -13 D. -13; -5; 0; 3; 17 Câu 6: Hoa gấp được 97 ngôi sao và xếp vào các hộp, mỗi hộp 8 ngôi sao. Số ngôi sao còn lại thừa không xếp vào hộp là: A. 1 ngôi sao B. 5 ngôi sao C. 6 ngôi sao D. 2 ngôi sao Câu 7: Diện tích của hình vuông có độ dài cạnh \(a = 4.5 + {2^2}.\left( {8 - 3} \right)\,\,\left( {cm} \right)\) là: A. \(160c{m^2}\) B. \(400c{m^2}\) C. \(40c{m^2}\) D. \(1600c{m^2}\) Câu 8: Hình bình hành không có tính chất nào dưới đây? A. Hai cạnh đối bằng nhau B. Hai cạnh đối song song với nhau C. Chu vi bằng chu vi hình chữ nhật D. Bốn cạnh bằng nhau Câu 9: Một đoàn khách du lịch gồm 52 người muốn qua sông nhưng mỗi chiếc thuyền chỉ chở được 6 người (kể cả người lái thuyền). Hỏi cần ít nhất bao nhiêu thuyền để chở hết số khách? A. 9 thuyền B. 10 thuyền C. 11 thuyền D. 12 thuyền Câu 10: Trong các câu sau, câu nào đúng? A. Tam giác đều có 6 trục đối xứng B. Hình chữ nhật có hai kích thước khác nhau có 4 trục đối xứng. C. Hình thang cân, góc ở đáy khác \({90^0}\), có đúng một trục đối xứng. D. Hình bình hành có hai trục đối xứng. Câu 11: Tổng hai số nguyên tố bằng 8. Tích hai số đó là A. 7 B. 15 C. 10 D. 12 Câu 12: Trong các phát biểu dưới đây, phát biểu nào đúng? A. Tam giác đều ABC là hình có tâm đối xứng. B. Hình bình hành MNPQ luôn nhận MP làm trục đối xứng. C. Hình bình hành luôn có 4 trục đối xứng. D. Hình thang cân luôn có trục đối xứng. II. TỰ LUẬN (7 điểm) Bài 1: (1,5 điểm) Thực hiện phép tính: a) \(152 - 274 - \left( { - 248} \right) + \left( { - 26} \right)\) b) \(\left( {87 - 37} \right):\left( { - 5} \right) + \left( {19 - 26} \right).{\left( { - 3} \right)^2}\) Bài 2: (1,5 điểm) Tìm x biết a) \(\left( { - 4} \right).x - 5 = 23 - 32\) b) \(\left( { - 34} \right):x + 15 = {\left( { - 5} \right)^2} + 2.\left( { - 4} \right)\) Bài 3: (1,5 điểm) Một đoàn y tế Hải Phòng vào tăng cường cho thành phố Đà Nẵng trong dịp phòng chống covit 19 gồm 72 bác sĩ và 120 điều dưỡng viên. Hỏi có thể chia đoàn y tế thành nhiều nhất bao nhiêu tổ (số bác sĩ và điều dưỡng viên được chia đều vào các tổ). Khi đó số bác sĩ và điều dưỡng viên của mỗi tổ là bao nhiêu? Bài 4: (2,0 điểm) Một mảnh sân nhà có hình dạng và kích thước như hình vẽ dưới đây.
a) Tính chu vi và diện tích mảnh sân. b) Nếu lát sân bằng những viên gạch hình vuông có cạnh 20 cm thì cần bao nhiêu viên gạch? Bài 5: (0,5 điểm) Chứng minh rằng \(A = 1 + 5 + {5^2} + \ldots + {5^{402}} + {5^{403}} + {5^{404}}\) chia hết cho \(31\). Lời giải Phần I: Trắc nghiệm
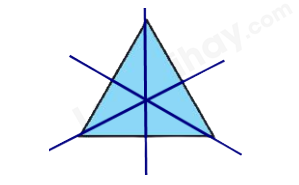
Câu 1 Phương pháp: Viết tập hợp A bằng cách liệt kê các phần tử. Cách giải: \(A = \left\{ {x \in \mathbb{N}|3 < x < 10} \right\}\) \( \Rightarrow A = \left\{ {4;5;6;7;8;9} \right\}\). Vậy tập hợp A có 6 phần tử. Chọn B. Câu 2 Phương pháp: Viết số tự nhiên bé nhất có ba chữ số và số tự nhiên lớn nhất có bốn chữ số. Thực hiện phép cộng. Cách giải: Số tự nhiên bé nhất có ba chữ số là 100. Số tự nhiên lớn nhất có bốn chữ số là 9999. Vậy tổng cửa số tự nhiên bé nhất có ba chữ số và số tự nhiên lớn nhất có bốn chữ số là: 100 + 9999 = 10 099 Chọn D. Câu 3 Phương pháp: Chia các trường hợp để xét dấu a, b. Từ đó tìm tích a.b lớn nhất. Cách giải: TH1: \(a > 0,\,\,b > 0 \Rightarrow a + b > 0\) (Không thỏa mãn) TH2: \(a = 0,\,\,b = - 1\) hoặc \(a = - 1,\,\,b = 0\). Khi đó \(a.b = 0\). TH3: \(a > 0,\,\,b < 0\) hoặc \(a < 0,\,\,b > 0\). Khi đó \(a.b < 0\). TH4: \(a < 0,\,\,b < 0 \Rightarrow a + b \le - 2\) (không thỏa mãn). Vậy tích a.b lớn nhất bằng 0. Chọn A. Câu 4 Phương pháp: Tính lũy thừa. Cách giải: \({\left( { - 3} \right)^3} = - 27\) Chọn C. Câu 5 Phương pháp: Sắp xếp các số nguyên theo thứ tự từ bé đến lớn. Cách giải: Sắp xếp các số nguyên 3; -13; 17; -5; 0 theo thứ tự tăng dần là: -13; -5; 0; 3; 17 Chọn D. Câu 6 Phương pháp: Tìm số dư của phép chia 97 cho 8. Cách giải: Ta có 97 : 8 = 12 dư 1. Vậy khi xếp 97 ngôi sao vào các hộp, mỗi hộp có 8 ngôi sao thì còn thừa 1 ngôi sao không xếp vào hộp. Chọn A. Câu 7 Phương pháp: Thực hiện phép tính tìm a. Diện tích hình vuông cạnh a bằng \({a^2}\). Cách giải: Ta có: \(\begin{array}{l}a = 4.5 + {2^2}.\left( {8 - 3} \right)\\a = 20 + 4.5\\a = 20 + 20\\a = 40\,\,\left( {cm} \right)\end{array}\) Vậy diện tích hình vuông có độ dài cạnh 40cm là: \({40^2} = 1600\,\,\left( {c{m^2}} \right)\). Chọn D. Câu 8 Phương pháp: Tính chất hình bình hành: Hình bình hành có các cạnh đối song song và bằng nhau. Cách giải: Hình bình hành có các cạnh đối song song và bằng nhau. Cả 4 cạnh chưa chắc bằng nhau nên đáp án D sai. Chọn D. Câu 9 Phương pháp: Thực hiện phép chia 52 cho 6. Số thuyền ít nhất bằng thương của phép chia trên cộng 1. Cách giải: Ta có: 52 : 6 = 8 dư 4. Vậy cần ít nhất 9 thuyền để chở hết số khách. Chọn A. Câu 10 Phương pháp: Vẽ các hình ở các đáp án và tìm trục đối xứng. Cách giải: Đáp án A sai: Tam giác đều có 3 trục đối xứng
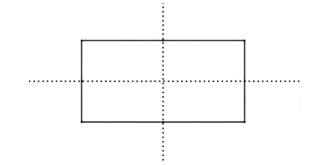
Đáp án B sai: Hình chữ nhật có hai kích thước khác nhau có 2 trục đối xứng.
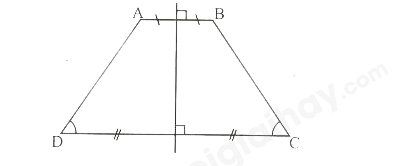
Đáp án C đúng: Hình thang cân, góc ở đáy khác \({90^0}\), có đúng một trục đối xứng.
Đáp án D sai: Hình bình hành không có trục đối xứng. Chọn C. Câu 11 Phương pháp: Số nguyên tố là số tự nhiên lớn hơn 1 có hai ước là 1 và chính nó. Tìm hai số nguyên tố có tổng bằng 8 và tìm tích. Cách giải: Hai số nguyên tố có tổng bằng 8 là 3 và 5. Tích của chúng là 3.5 = 15. Chọn B. Câu 12 Phương pháp: Tam giác đều là hình có trục đối xứng chứ không có tâm đối xứng. Hình bình hành không có trục đối xứng. Cách giải: Tam giác đều là hình có trục đối xứng chứ không có tâm đối xứng nên đáp án A sai. Hình bình hành không có trục đối xứng nên đáp án B, C sai. Chọn D. II. TỰ LUẬN (7 điểm) Bài 1 Phương pháp: Thực hiện đúng thứ tự thực hiện phép tính. Nhóm để phù hợp và tính được nhanh hơn. Cách giải: a) \(\begin{array}{l}\,\,\,\,152 - 274 - \left( { - 248} \right) + \left( { - 26} \right)\\ = 152 - 274 + 248 - 26\\ = \left( {152 + 248} \right) - \left( {274 + 26} \right)\\ = 400 - 300\\ = 100\end{array}\) b) \(\begin{array}{l}\,\,\,\,\left( {87 - 37} \right):\left( { - 5} \right) + \left( {19 - 26} \right).{\left( { - 3} \right)^2}\\ = 50:\left( { - 5} \right) + \left( { - 7} \right).9\\ = - 10 - 63\\ = - 73\end{array}\) Bài 2 Phương pháp: Thực hiện đúng thứ tự thực hiện phép tính. Nhóm để phù hợp và tính được nhanh hơn. Cách giải: a) \(\begin{array}{l}\left( { - 4} \right).x - 5 = 23 - 32\\\left( { - 4} \right).x - 5 = - 9\\\left( { - 4} \right).x\,\,\,\,\,\,\,\,\, = - 9 + 5\\\left( { - 4} \right).x\,\,\,\,\,\,\,\,\, = - 4\\\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\, = - 4:\left( { - 4} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\, = 1\end{array}\) b) \(\begin{array}{l}\left( { - 34} \right):x + 15 = {\left( { - 5} \right)^2} + 2.\left( { - 4} \right)\\\left( { - 34} \right):x + 15 = 25 + 2.\left( { - 4} \right)\\\left( { - 34} \right):x + 15 = 25 + \left( { - 8} \right)\\\left( { - 34} \right):x + 15 = 17\\\left( { - 34} \right):x\,\,\,\,\,\,\,\,\,\,\, = 17 - 15\\\left( { - 34} \right):x\,\,\,\,\,\,\,\,\,\,\, = 2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = \left( { - 34} \right):2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = - 17\end{array}\) Bài 3 Phương pháp: Thực hiện bài toán tìm ƯCLN(72;120). Cách giải: Gọi có thể chia được nhiều nhất x tổ \(\left( {x \in {\mathbb{N}^*}} \right)\). Theo đề bài ra ta có \(x\,\, \vdots \,\,72\), \(x\,\, \vdots \,\,120\) và x là số tự nhiên lớn nhất, nên \(x = UCLN\left( {72;120} \right)\). Ta có: \(\begin{array}{l}72 = {2^3}{.3^2}\\120 = {2^3}.3.5\end{array}\) \( \Rightarrow UCLN\left( {72;120} \right) = {2^3}.3 = 24\). Vậy có thể chia nhiều nhất là 24 tổ. Khi đó mỗi tổ có: \(120:24 = 5\) (điều dưỡng) \(72:24 = 3\) (bác sĩ). Bài 4 Phương pháp: a) Chia mảnh vườn thành những hình vuông, hình chữ nhật và tính diện tích. b) Tính diện tích 1 viên gạch. Tính số viên gạch = diện tích mảnh vườn : diện tích 1 viên gạch. Cách giải:
a) Chia mảnh vườn thành 2 phần như hình vẽ. Diện tích mảnh vườn 1 là: \(10.5 = 50\,\,\left( {{m^2}} \right)\) Diện tích mảnh vườn 2 là: \(20.4 = 80\,\,\left( {{m^2}} \right)\) Diện tích mảnh vườn là: \(50 + 80 = 130\,\,\left( {{m^2}} \right)\). b) Diện tích viên gạch hình vuông 20cm là: \(20.20 = 400\,\,\left( {c{m^2}} \right) = 0,04\,\,\left( {{m^2}} \right)\) Số viên gạch cần là: \(130:0,04 = 3250\) (viên gạch). Bài 5 Phương pháp: Sử dụng tính chất chia hết cho một tích, tổng. Cách giải: a) Chứng minh rằng \(A = 1 + 5 + {5^2} + \ldots + {5^{402}} + {5^{403}} + {5^{404}}\) chia hết cho \(31\). \(\begin{array}{l}A = 1 + 5 + {5^2} + \ldots + {5^{402}} + {5^{403}} + {5^{404}}\\A = \left( {1 + 5 + {5^2}} \right) + \left( {{5^3} + {5^4} + {5^5}} \right) + \ldots + \left( {{5^{402}} + {5^{403}} + {5^{404}}} \right)\\A = \left( {1 + 5 + {5^2}} \right) + {5^3}.\left( {1 + 5 + {5^2}} \right) + \ldots + {5^{402}}.\left( {1 + 5 + {5^2}} \right)\\A = \left( {1 + 5 + {5^2}} \right).\left( {1 + {5^3} + \ldots + {5^{402}}} \right)\\A = 31.\left( {1 + {5^3} + \ldots + {5^{402}}} \right)\,\, \vdots \,\,31\\ \Rightarrow A\,\, \vdots \,\,31\end{array}\)
|