Đề thi học kì 1 Toán 6 - Đề số 17Phần trắc nghiệm (2 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x < 2} \right\}\). Tập hợp A viết dưới dạng liệt kê các phần tử là:
Câu 2 :
Bội chung nhỏ nhất của 12 và 36 là:
Câu 3 :
Số đối của số 53 là:
Câu 5 :
Các số 2; 9; 0; -15; -4 được sắp xếp theo thứ tự giảm dần là
Câu 8 :
Trong các hình sau, hình nào có các góc đều bằng \(60^\circ \)?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x < 2} \right\}\). Tập hợp A viết dưới dạng liệt kê các phần tử là:
Đáp án : A Phương pháp giải :
Liệt kê các số nguyên thỏa mãn \( - 2 \le x < 2\). Lời giải chi tiết :
Tập hợp \(A = \left\{ { - 2; - 1;0;1} \right\}\). Đáp án A
Câu 2 :
Bội chung nhỏ nhất của 12 và 36 là:
Đáp án : C Phương pháp giải :
Kiểm tra 36 chia hết cho 12. Lời giải chi tiết :
Vì 36 chia hết cho 12 nên bội chung nhỏ nhất của 12 và 36 là 36. Đáp án C
Câu 3 :
Số đối của số 53 là:
Đáp án : A Phương pháp giải :
Số đối của a là –a. Lời giải chi tiết :
Số đối của 53 là -53. Đáp án A
Đáp án : C Phương pháp giải :
So sánh các số nguyên âm: Nếu a và b là các số nguyên dương và a > b thì –a < -b. Lời giải chi tiết :
Vì 87 < 184 < 220 < 224 nên -87 > -184 > -220 > -224. Vậy hành tinh có nhiệt độ thấp nhất là Sao Thiên Vương (\( - 224^\circ C\)). Đáp án C
Câu 5 :
Các số 2; 9; 0; -15; -4 được sắp xếp theo thứ tự giảm dần là
Đáp án : B Phương pháp giải :
Chia làm 2 nhóm: các số nguyên dương và nguyên âm để so sánh. Lời giải chi tiết :
Ta chia các số thành hai nhóm: + Nhóm 1: 2; 9. Ta có: 2 < 9. + Nhóm 2: -15; -4. Ta có: 4 < 15 nên -4 > -15. Vậy các số sắp xếp theo thứ tự giảm dần là 9; 2; 0; -4; -15. Đáp án B
Đáp án : A Phương pháp giải :
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình. Lời giải chi tiết :
Hình có tâm đối xứng là hình 1. Đáp án A
Đáp án : C Phương pháp giải :
Hình thoi là hình có 4 cạnh bằng nhau. Lời giải chi tiết :
Hình 3 là hình thoi. Đáp án C
Câu 8 :
Trong các hình sau, hình nào có các góc đều bằng \(60^\circ \)?
Đáp án : C Phương pháp giải :
Lời giải chi tiết :
Hình có các góc đều bằng \(60^\circ \) là tam giác đều. Đáp án C
II. Tự luận
Phương pháp giải :
a) Sử dụng quy tắc cộng hai số nguyên khác dấu. Để cộng hai số nguyên khác dấu, ta làm như sau: Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại. Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn. Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm. b) Tính lũy thừa, áp dụng tính chất phân phối của phép nhân với phép cộng để tính. c) Phá ngoặc sau đó sử dụng tính chất của kết hợp của phép cộng để nhóm. d) Sử dụng các quy tắc tính với số nguyên và thứ tự thực hiện phép tính: Nếu biểu thức có các dấu ngoặc: ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: ( ) → [ ] → { } Lời giải chi tiết :
a) \( - 132 + 125\)\( = - \left( {132 - 125} \right) = - 7\) b) \({2^3}.\left( { - 135} \right) + {35.2^3}\) \(\begin{array}{l} = 8.\left( { - 135} \right) + 35.8\\ = 8\left( { - 135 + 35} \right)\\ = 8.\left( { - 100} \right)\\ = - 800\end{array}\) c) \(\left[ {\left( { - 235} \right) + 171} \right] - \left( {71 - 235} \right)\) \(\begin{array}{l} = - 235 + 171 - 71 - 235\\ = \left( { - 235 + 235} \right) + \left( {171 - 71} \right)\\ = 0 + 100\\ = 100\end{array}\) d) \(160:\left\{ {17 + \left[ {{3^2}.5 - \left( {14 + {2^{11}}:{2^8}} \right)} \right]} \right\}\) \(\begin{array}{l} = 160:\{ 17 + [{3^2}.5 - (14 + {2^3})]\} \\ = 160:\left\{ {17 + \left[ {9.5 - \left( {14 + 8} \right)} \right]} \right\}\\ = 160:\left\{ {17 + \left[ {45 - 22} \right]} \right\}\\ = 160:\left\{ {17 + 23} \right\}\\ = 160:40\\ = 4\end{array}\) Phương pháp giải :
a) Muốn tìm một số hạng trong một tổng ta lấy tổng trừ đi số hạng còn lại. b) Áp dụng quy tắc chuyển vế để tìm x. c) Áp dụng quy tắc chuyển vế để tìm x. Lời giải chi tiết :
a) \(x - 10 = - 65\) \(\begin{array}{l}x = - 65 + 10\\x = - 55\end{array}\) Vậy \(x = - 55\) b) \(32:\left( {x + 125} \right) = - {4^2}\) \(\begin{array}{l}32:\left( {x + 125} \right) = - 16\\x + 125 = 32:\left( { - 16} \right)\\x + 125 = - 2\\x = - 2 - 125\\x = - 127\end{array}\) Vậy \(x = - 127\) c) \(20 - 5\left( {2 - x} \right) = 45\) \(\begin{array}{l}5\left( {2 - x} \right) = 20 - 45\\5\left( {2 - x} \right) = - 25\\2 - x = - 25:5\\2 - x = - 5\\x = 2 - \left( { - 5} \right)\\x = 7\end{array}\) Vậy \(x = 7\). Phương pháp giải :
Gọi số học sinh của trường là \(x\) (học sinh, \(x \in {\mathbb{N}^*},1200 \le x \le 1500\)) Lập luận \(x \in BC\left( {36;40;48} \right)\) Phân tích 36; 40; 48 để tìm BCNN(36;40;48) Kết hợp điều kiện của \(x\). Lời giải chi tiết :
Gọi số học sinh của trường là \(x\) (học sinh, \(x \in {\mathbb{N}^*},1200 \le x \le 1500\)) Vì nếu xếp mỗi xe ô tô 36 học sinh; 40 học sinh hoặc 48 học sinh thì đều đủ chỗ nên \(x \vdots 36;x \vdots 40;x \vdots 48\), hay \(x \in BC\left( {36;40;48} \right)\). Ta có: \(36 = {2^2}{.3^2}\) \(40 = {2^3}.5\) \(48 = {2^4}.3\) Suy ra \(BCNN\left( {36;40;48} \right) = {2^4}{.3^2}.5 = 720\) Do đó \(BC\left( {36;40;48} \right) = \left\{ {0;720;1440;2160;...} \right\}\) Vì \(1200 \le x \le 1500\) nên \(x = 1440\) (TMĐK) Vậy số học sinh của trường là 1440 học sinh. Phương pháp giải :
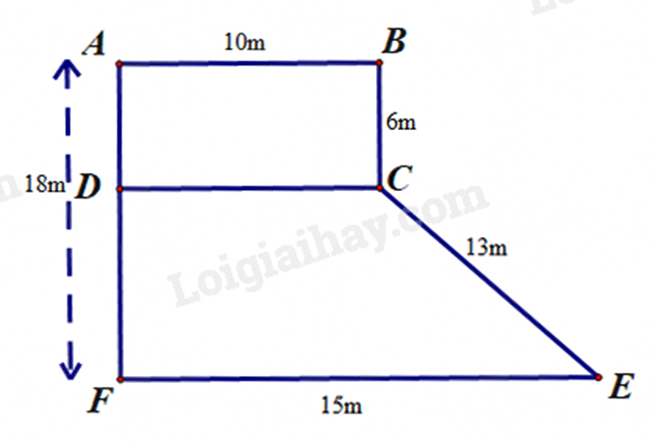
a) Áp dụng công thức tính diện tích phần vườn hình chữ nhật = chiều dài . chiều rộng. b) Tính chu vi của mảnh vườn. Chiều dài hàng rào chính là chu vi của mảnh vườn. c) Tính diện tích phần vườn hình thang = tổng hai đáy . chiều cao : 2. Tính diện tích vườn bằng tổng diện tích phần vườn hình chữ nhật và phần vườn hình thang. Phương án 1. Tính doanh thu khi trồng mía trên cả mảnh vườn. Phương án 2. Tính doanh thu trồng ngô + doanh thu trồng thanh long. Doanh thu = diện tích . số tiền thu được trên 1 mét vuông. Lời giải chi tiết :
a) Diện tích phần vườn hình chữ nhật là: \(10.6 = 60\left( {{m^2}} \right)\) b) Chiều dài hàng rào là: \(10 + 6 + 13 + 15 + 18 = 62\left( m \right)\) c) Chiều cao phần vườn hình thang là: \(18 - 6 = 12\left( m \right)\) Diện tích phần vườn hình thang là: \(\left( {10 + 15} \right).12:2 = 150\left( {{m^2}} \right)\) Tổng diện tích mảnh vườn là: \(60 + 150 = 210\left( {{m^2}} \right)\) - Doanh thu theo phương án 1 là: \(210.30 = 6300\) (nghìn đồng) - Doanh thu theo phương án 2 là: \(25.150 + 40.60 = 6150\) (nghìn đồng) Vậy bác Khánh chọn phương án 1 sẽ có doanh thu tốt hơn. Phương pháp giải :
Hai số nguyên tố cùng nhau nếu ước chung lớn nhất của chúng bằng 1. Giả sử ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)). Chứng minh d = 1 nên \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau. Lời giải chi tiết :
Gọi ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)). Suy ra \(2n + 1 \vdots d\); \(3n + 1 \vdots d\). Do đó \(3\left( {2n + 1} \right) \vdots d\); \(2\left( {3n + 1} \right) \vdots d\) hay \(6n + 3 \vdots d\); \(6n + 2 \vdots d\) Suy ra \(\left( {6n + 3} \right) - \left( {6n + 2} \right) \vdots d\) hay \(1 \vdots d\) suy ra d \( \in \) Ư(1) = {1; -1} Mà \(d \in \mathbb{N}\) nên d = 1. Do đó ƯCLN(2n+1;3n+1) = 1 Vậy \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.
|