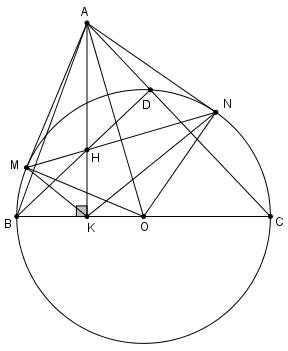
Đề số 12 - Đề thi vào lớp 10 môn ToánĐề thi vào lớp 10 môn Toán - Đề số 12 có đáp án và lời giải chi tiết Đề bài Câu 1 (2,5 điểm) a) Rút gọn biểu thức: \(P = 3\sqrt 5 + \sqrt {20} .\) b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x + 2y = 5\\x - y = 2\end{array} \right..\) c) Tìm giá trị của tham số m để đồ thị hàm số \(y = x + m\) đi qua điểm \(A\left( {0;\;3} \right).\) Câu 2 (2 điểm) Cho phương trình \({x^2} - mx + m - 4 = 0\;\;\left( 1 \right),\) (x là ẩn số và m là tham số). a) Giải phương trình (1) khi \(m = 8.\) b) Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) với mọi \(m.\) Tìm tất cả các giá trị nguyên dương của \(m\) để \(\left( {5{x_1} - 1} \right)\left( {5{x_2} - 1} \right) < 0.\) Câu 3 (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình. Một hình chữ nhật có chu vi bằng 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật, biết rằng nếu tăng chiều dài thêm 1 cm và tăng chiều rộng thêm 2 cm thì diện tích của hình chữ nhật đó tăng thêm 25 cm2. Câu 4 (3,5 điểm) Cho tam giác ABC nhọn có AB < AC và đường cao AK. Vẽ đường tròn tâm O đường kính BC. Từ A kẻ các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm, M và B nằm trên cùng nửa mặt phẳng có bờ là đường thẳng AO). Gọi H là giao điểm của hai đường thẳng MN và AK. Chứng minh rằng: a) Tứ giác AMKO nội tiếp đường tròn. b) KA là tia phân giác của góc MKN. c) \(A{N^2} = AK.AH\) Bài 5 (0,5 điểm) Cho a, b là hai số thực dương thỏa mãn \(a + b \le 4\). Tìm giá trị nhỏ nhất của biểu thức \(S = \dfrac{1}{{{a^2} + {b^2}}} + \dfrac{{25}}{{ab}} + ab\) Lời giải chi tiết Câu 1: a) Rút gọn biểu thức: \(P = 3\sqrt 5 + \sqrt {20} .\) \(P = 3\sqrt 5 + \sqrt {20} = 3\sqrt 5 + \sqrt {{2^2}.5} \)\(\,= 3\sqrt 5 + 2\sqrt 5 = 5\sqrt 5 .\) Vậy \(P = 5\sqrt 5 .\) b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x + 2y = 5\\x - y = 2\end{array} \right..\) \(\left\{ \begin{array}{l}x + 2y = 5\\x - y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3y = 3\\x = y + 2\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = y + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right..\) Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\;y} \right) = \left( {3;\;1} \right).\) c) Tìm giá trị của tham số m để đồ thị hàm số \(y = x + m\) đi qua điểm \(A\left( {0;\;3} \right).\) Đồ thị hàm số \(y = x + m\) đi qua điểm \(A\left( {0;\;3} \right)\) nên ta có: \(3 = 0 + m \Leftrightarrow m = 3.\) Vậy \(m = 3\) thỏa mãn điều kiện bài toán. Câu 2: Cho phương trình \({x^2} - mx + m - 4 = 0\;\;\left( 1 \right),\) (x là ẩn số và m là tham số). a) Giải phương trình (1) khi \(m = 8.\) Thay \(m = 8\) vào phương trình ta được: \(\begin{array}{l}\left( 1 \right) \Leftrightarrow {x^2} - 8x + 8 - 4 = 0\\ \Leftrightarrow {x^2} - 8x + 4 = 0.\end{array}\) Có: \(\Delta ' = {4^2} - 4 = 12 > 0\) \( \Rightarrow \sqrt {\Delta '} = \sqrt {12} = 2\sqrt 3 .\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = 4 + 2\sqrt 3 \\{x_2} = 4 - 2\sqrt 3 \end{array} \right..\) Vậy với \(m = 8\) thì phương trình có tập nghiệm \(S = \left\{ {4 - 2\sqrt 3 ;4 + 2\sqrt 3 } \right\}.\) b) Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) với mọi \(m.\) Tìm tất cả các giá trị nguyên dương của \(m\) để \(\left( {5{x_1} - 1} \right)\left( {5{x_2} - 1} \right) < 0.\) \({x^2} - mx + m - 4 = 0\;\;\left( 1 \right),\) Ta có: \(\Delta = {m^2} - 4\left( {m - 4} \right) = {m^2} - 4m + 16 \)\(\,= {\left( {m - 2} \right)^2} + 12 > 0\;\;\forall m.\) \( \Rightarrow \) Phương trình (1) có hai nghiệm phân biệt \({x_1},\;{x_2}\) với mọi \(m.\) Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = m - 4\end{array} \right..\) Theo đề bài ta có: \(\left( {5{x_1} - 1} \right)\left( {5{x_2} - 1} \right) < 0\) \(\begin{array}{l} \Leftrightarrow 25{x_1}{x_2} - 5\left( {{x_1} + {x_2}} \right) + 1 < 0\\ \Leftrightarrow 25\left( {m - 4} \right) - 5m + 1 < 0\\ \Leftrightarrow 20m < 99\\ \Leftrightarrow m < \dfrac{{99}}{{20}} = 4,95.\end{array}\) Vậy \(m \in {Z^ + }\) thỏa mãn bài toán là: \(m \in \left\{ {1;\;2;\;3;\;4} \right\}.\) Câu 3: Một hình chữ nhật có chu vi bằng 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật, biết rằng nếu tăng chiều dài thêm 1 cm và tăng chiều rộng thêm 2 cm thì diện tích của hình chữ nhật đó tăng thêm 25 cm2. Gọi chiều dài của hình chữ nhật là \(x\;\left( {cm} \right),\) chiều rộng của hình chữ nhật là \(y\left( {cm} \right),\;\;\left( {0 < y < x < 14} \right).\) Nửa chu vi của hình chữ nhật là: \(x + y = 28:2 \Leftrightarrow x + y = 14\;\;\;\;\left( 1 \right).\) Diện tích của hình chữ nhật ban đầu là: \(xy\;\;\left( {c{m^2}} \right).\) Chiều dài mới của hình chữ nhật sau khi tăng thêm \(1\;cm\) là \(x + 1\;\;\left( {cm} \right).\) Chiều rộng mới của hình chữ nhật sau khi tăng thêm \(2\;cm\) là \(y + 2\;\;\left( {cm} \right).\) Diện tích của hình chữ nhật sau khi tăng chiều dài và chiều rộng là: \(\left( {x + 1} \right)\left( {y + 2} \right) = xy + 2x + y + 2\)\(\;\;\left( {c{m^2}} \right).\) Theo đề bài ta có phương trình: \(xy + 2x + y + 2 = xy + 25 \)\(\,\Leftrightarrow 2x + y = 23\;\;\;\left( 2 \right).\) Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 14\\2x + y = 23\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 9\\y = 14 - x\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}x = 9\;\;\;\left( {tm} \right)\\y = 5\;\;\;\left( {tm} \right)\end{array} \right..\) Vậy chiều dài hình chữ nhật ban đầu là \(9\;cm,\) chiều rộng là \(5\;cm.\) Câu 4. a) Tứ giác AMKO nội tiếp đường tròn. Ta có : \(\widehat {AMO} = {90^o}\) (Do AM là tiếp tuyến của đường tròn tâm O tại M) Ta có \(\widehat {AMO} = \widehat {AKO} = {90^0}\) (gt) \( \Rightarrow \) Tứ giác AMKO có hai đỉnh M, K kề nhau cùng nhìn cạnh AO dưới 1 góc 900 \( \Rightarrow \) Tứ giác AMKO là tứ giác nội tiếp (Tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau). b) KA là tia phân giác của góc MKN. Ta có : \(\widehat {ANO} = {90^o}\) (Do AN là tiếp tuyến của đường tròn tâm O tại N) Xét tứ giác ANOK có \(\widehat {ANO} + \widehat {AKO} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác ANOK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800) Tứ giác AMKO nội tiếp \( \Rightarrow \widehat {AKM} = \widehat {AOM}\) (hai góc nội tiếp cùng chắn cung AM) Tứ giác ANOK nội tiếp \( \Rightarrow \widehat {AKN} = \widehat {AON}\) (hai góc nội tiếp cùng chắn cung AN) Mà \(\widehat {AOM} = \widehat {AON}\) (tính chất hai tiếp tuyến AM và AN cắt nhau tại A). \( \Rightarrow \widehat {AKM} = \widehat {AKN}\) \(\Rightarrow KA\) là phân giác của góc MKN. c) \(A{N^2} = AK.AH\) Ta có \(AM = AN\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow A\) thuộc trung trực của MN. \(OM = ON\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của MN. \( \Rightarrow OA\) là trung trực của MN \( \Rightarrow OA \bot MN\). \( \Rightarrow \widehat {AMN} = \widehat {AOM}\) (cùng phụ với góc OAM). Mà \(\widehat {AKM} = \widehat {AOM}\,\,\left( {cmt} \right)\) \(\Rightarrow \widehat {AKM} = \widehat {AMN} = \widehat {AMH}\) Xét tam giác AMH và tam giác AKM có : \(\widehat {MAK}\) chung ; \(\widehat {AKM} = \widehat {AMH}\,\,\left( {cmt} \right)\) ; \( \Rightarrow \Delta AMH \sim \Delta AKM\,\,\left( {g.g} \right) \) \(\Rightarrow \dfrac{{AM}}{{AH}} = \dfrac{{AK}}{{AM}}\) \(\Rightarrow A{M^2} = AH.AK\) Mà \(AM = AN\,\,\left( {cmt} \right)\) \(\Rightarrow A{N^2} = AH.AK\) Câu 5. Cách giải : Áp dụng BĐT : \({\left( {a + b} \right)^2} \ge 4ab \Leftrightarrow \dfrac{{a + b}}{{ab}} \ge \dfrac{4}{{a + b}} \) \(\Leftrightarrow \dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\) \(\begin{array}{l}S = \dfrac{1}{{{a^2} + {b^2}}} + \dfrac{{25}}{{ab}} + ab\\S = \dfrac{1}{{{a^2} + {b^2}}} + \dfrac{1}{{2ab}} + \dfrac{{49}}{{2ab}} + ab\\S \ge \dfrac{4}{{{a^2} + {b^2} + 2ab}} + \dfrac{{49}}{{2ab}} + ab\\S \ge \dfrac{4}{{{{\left( {a + b} \right)}^2}}} + \dfrac{{17}}{{2ab}} + \dfrac{{16}}{{ab}} + ab\end{array}\) Ta có \(2\sqrt {ab} \le a + b\) \(\Leftrightarrow ab \le \dfrac{{{{\left( {a + b} \right)}^2}}}{4} \le 4\) \(\Rightarrow \dfrac{4}{{{{\left( {a + b} \right)}^2}}} \ge \dfrac{1}{4}\) \( \Rightarrow S \ge \dfrac{1}{4} + \dfrac{{17}}{{2.4}} + 2\sqrt {\dfrac{{16}}{{ab}}.ab} = \dfrac{{83}}{8}\) Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a + b = 4\\a = b\\ab = 4\end{array} \right. \Leftrightarrow a = b = 2\). Vậy \({S_{\min }} = \dfrac{{83}}{8}\), đạt tại \(a = b = 2\). HocTot.XYZ
|