Đề thi giữa kì 2 Toán 8 - Đề số 1 - Chân trời sáng tạoPhần trắc nghiệm (3 điểm) Câu 1: (150973) Cho hàm số $y=f(x)=-{{x}^{2}}+2.$ Tính $fleft( frac{-1}{2} right);fleft( 0 right)$ .Đề bài
I. Trắc nghiệm
Khoanh tròn trước câu trả lời đúng.
Câu 1 :
Cho hàm số \(y = f(x) = - {x^2} + 2.\) Tính \(f\left( {\frac{{ - 1}}{2}} \right);f\left( 0 \right)\) .
Câu 2 :
Một cửa hàng gạo nhập vào kho 480 tấn. Mỗi ngày bán đi 20 tấn. Gọi y (tấn) là số gạo còn lại sau x (ngày) bán. Công thức biểu diễn y theo x là :
Câu 4 :
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = 6 - 2x\)?
Câu 5 :
Đường thẳng song song với đường thẳng y = 3x và cắt trục tung tại điểm có tung độ bằng 2 là:
Câu 6 :
Cho hai đường thẳng \(y = - \frac{1}{3}x + 2\) và \(y = \frac{1}{3}x + 2\). Hai đường thẳng đã cho:
Câu 7 :
Cho AB = 16cm. CD = 3dm. Tỉ số \(\frac{{AB}}{{CD}}\) là:
Câu 10 :
Cho tam giác ABC, vẽ MN//BC sao cho AN =\(\frac{1}{2}\)AB, M \( \in \) AB, N \( \in \) AC. Biết AN = 2cm, AM = 1cm, thì AC bằng:
Câu 11 :
Có bao nhiêu đường trung bình trong một tam giác?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Khoanh tròn trước câu trả lời đúng.
Câu 1 :
Cho hàm số \(y = f(x) = - {x^2} + 2.\) Tính \(f\left( {\frac{{ - 1}}{2}} \right);f\left( 0 \right)\) .
Đáp án : B Phương pháp giải :
Thay \(x = \frac{{ - 1}}{2}\) và x = 0 vào hàm số để tính giá trị. Lời giải chi tiết :
Ta có: \(\begin{array}{l}f\left( {\frac{{ - 1}}{2}} \right) = - {\left( {\frac{{ - 1}}{2}} \right)^2} + 2 = - \frac{1}{4} + 2 = \frac{7}{4}\\f\left( 0 \right) = - {0^2} + 2 = 2\end{array}\)
Câu 2 :
Một cửa hàng gạo nhập vào kho 480 tấn. Mỗi ngày bán đi 20 tấn. Gọi y (tấn) là số gạo còn lại sau x (ngày) bán. Công thức biểu diễn y theo x là :
Đáp án : A Phương pháp giải :
Biểu diễn y theo x. Lời giải chi tiết :
Số gạo ban đầu là 480 tấn. Mỗi ngày của hàng bán được 20 tấn thì x ngày cửa hạng bán được 20.x (tấn). => Sau x ngày bán, cửa hàng còn lại: 480 – 20x (tấn). Vậy ta có công thức biểu diễn y theo x là: y = 480 – 20x.
Đáp án : A Phương pháp giải :
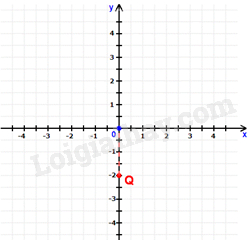
Quan sát đồ thị để xác định tọa độ điểm Q. Lời giải chi tiết :
Điểm Q thuộc trục tung nên có hoành độ bằng 0 và hình chiếu của điểm Q trên trục tung là -2 nên \(Q\left( {0; - 2} \right)\).
Câu 4 :
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = 6 - 2x\)?
Đáp án : C Phương pháp giải :
Thay tọa độ điểm vào hàm số để xác định. Lời giải chi tiết :
Ta có: \(6 - 2.2 = 2 \ne - 2 \Rightarrow \left( {2; - 2} \right)\) không thuộc đồ thị hàm số \(y = 6 - 2x\). \(6 - 2.6 = - 6 \ne 0 \Rightarrow \left( {6;0} \right)\) không thuộc đồ thị hàm số \(y = 6 - 2x\). \(6 - 2.0 = 6 \Rightarrow \left( {0;6} \right)\) thuộc đồ thị hàm số \(y = 6 - 2x\). \(6 - 2.\left( { - 3} \right) = 12 \ne 0 \Rightarrow \left( { - 3;0} \right)\) không thuộc đồ thị hàm số \(y = 6 - 2x\).
Câu 5 :
Đường thẳng song song với đường thẳng y = 3x và cắt trục tung tại điểm có tung độ bằng 2 là:
Đáp án : C Phương pháp giải :
Hai đường thẳng song song có hệ số góc bằng nhau. Thay tọa độ điểm để tìm đường thẳng. Lời giải chi tiết :
Đường thẳng song song với đường thẳng y = 3x có dạng y = 3x + b. Đường thẳng này cắt trục tung tại điểm có tung độ bằng 2 nên đường thẳng đi qua điểm (0; 2) \( \Rightarrow 2 = 3.0 + b \Rightarrow b = 2\). Đường thẳng cần tìm là y = 3x + 2.
Câu 6 :
Cho hai đường thẳng \(y = - \frac{1}{3}x + 2\) và \(y = \frac{1}{3}x + 2\). Hai đường thẳng đã cho:
Đáp án : B Phương pháp giải :
Dựa vào vị trí tương đối của hai đường thẳng. Lời giải chi tiết :
Ta có \( - \frac{1}{3} \ne \frac{1}{3}\) nên hai đường thẳng cắt nhau. Xét phương trình hoành độ giao điểm hai đường thẳng, ta có: \(\begin{array}{l} - \frac{1}{3}x + 2 = \frac{1}{3}x + 2\\ - \frac{2}{3}x = 0\\x = 0\end{array}\) \( \Rightarrow y = \frac{1}{3}.0 + 2 = 2\) Vậy hai đường thẳng đã cho cắt nhau tại điểm có tung độ là 2.
Câu 7 :
Cho AB = 16cm. CD = 3dm. Tỉ số \(\frac{{AB}}{{CD}}\) là:
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về tỉ số giữa hai đoạn thẳng. Lời giải chi tiết :
Đổi 3dm = 30cm. Tỉ số \(\frac{{AB}}{{CD}} = \frac{{16}}{{30}} = \frac{8}{{15}}\).
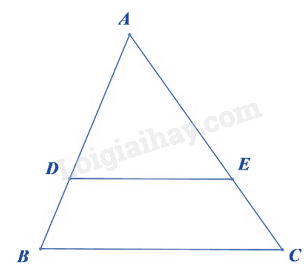
Đáp án : C Phương pháp giải :
Dựa vào định lí Thales đảo trong tam giác. Lời giải chi tiết :
Theo định lí đảo trong tam giác, nếu \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}} \Rightarrow DE//BC\).
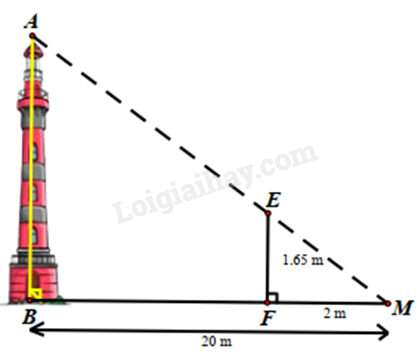
Đáp án : A Phương pháp giải :
Dựa vào hệ quả của định lí Thales để tính AB. Lời giải chi tiết :
Vì EF // AB nên \(\frac{{AB}}{{EF}} = \frac{{BM}}{{MF}}\)\( \Rightarrow AB = \frac{{BM.EF}}{{MF}} = \frac{{20.1,65}}{2} = 16,5\left( m \right)\)
Câu 10 :
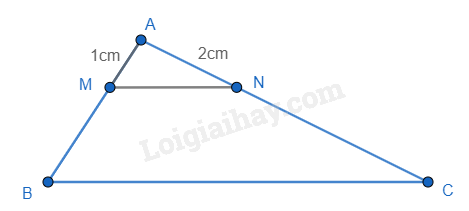
Cho tam giác ABC, vẽ MN//BC sao cho AN =\(\frac{1}{2}\)AB, M \( \in \) AB, N \( \in \) AC. Biết AN = 2cm, AM = 1cm, thì AC bằng:
Đáp án : C Phương pháp giải :
Áp dụng định lí Thalès để tính BC. Lời giải chi tiết :
Vì AN = \(\frac{1}{2}\)AB nên AB = 2.AN = 2.2 = 4(cm). Ta có MN // BC. Áp dụng định lí Thales, ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Leftrightarrow \frac{1}{4} = \frac{2}{{AC}} \Leftrightarrow AC = 4.2 = 8\) (cm). Vậy AC = 8cm.
Câu 11 :
Có bao nhiêu đường trung bình trong một tam giác?
Đáp án : C Phương pháp giải :
Sử dụng khái niệm đường trung bình. Lời giải chi tiết :
Xét tam giác ABC bất kì. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.
MN là đường trung bình của tam giác ABC. NP là đường trung bình của tam giác ABC. MP là đường trung bình của tam giác ABC. Vậy có 3 đường trung bình trong một tam giác.
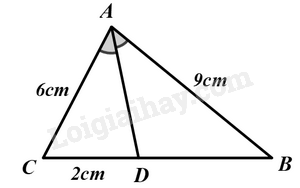
Đáp án : D Phương pháp giải :
Sử dụng tính chất của đường phân giác trong tam giác. Lời giải chi tiết :
Ta có AD là tia phân giác của góc A nên \(\frac{{AB}}{{BD}} = \frac{{AC}}{{CD}} \Leftrightarrow \frac{9}{{BD}} = \frac{6}{2} = 3\) \( \Rightarrow BD = \frac{9}{3} = 3\)(cm)
II. Tự luận
Phương pháp giải :
a) Lấy hai điểm thuộc đồ thị hàm số, đồ thị hàm số là đường thẳng đi qua hai điểm đó. b) Viết phương trình hoành độ giao điểm hai đồ thị hàm số đó để tìm giao điểm. c) Dựa vào vị trí tương đối của hai đường thẳng để xác định a. Thay tọa độ điểm B vào hàm số để tìm b. Lời giải chi tiết :
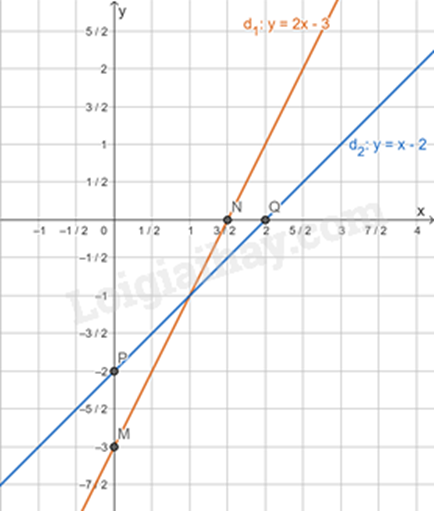
a) +) Với hàm số \(y = 2x - 3\): Cho x = 0 thì y = -3. Cho y = 0 thì x = \(\frac{3}{2}\). Đồ thị của hàm số \(y = 2x - 3\) là đường thẳng đi qua hai điểm \(M\left( {0; - 3} \right)\) và \(N\left( {\frac{3}{2};0} \right)\). +) Với hàm số \(y = x - 2\): Cho x = 0 thì y = -2. Cho y = 0 thì x = 2. Đồ thị của hàm số \(y = x - 2\) là đường thẳng đi qua hai điểm \(P\left( {0; - 2} \right)\) và \(Q\left( {2;0} \right)\). Ta có đồ thị của hai hàm số:
b) Xét phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x – 3 và y = x – 2, ta có: \(\begin{array}{l}2x - 3 = x - 2\\2x - x = - 2 + 3\\x = 1\\ \Rightarrow y = 1 - 2 = - 1\end{array}\) Vậy tọa độ giao điểm của hai đồ thị hai hàm số là A(1; -1). c) Ta có: \( d_3 \parallel d_1\) nên \(d_3 \) có dạng \( y = 2x + b \). Điểm có hoành độ bằng - 1 thuộc đường thẳng \( d_2: y = x - 2 \) là: B(-1; -1 - 2) hay B(-1; -3) Vì \( d_3 \) cắt đường thẳng \( d_2: y = x - 2 \) tại điểm có hoành độ bằng -1, nên toạ độ giao điểm là B(-1; -3) Thay tọa độ điểm \( B(-1; -3) \) vào phương trình \( y = 2x + b \), ta có: \(b = -3 + 2\) \(b = -1\) Phương pháp giải :
a) Tìm t ứng với năm 2023. Thay t vào hàm số để tính diện tích rừng Sác được phủ xanh vào năm 2023. b) Thay S = 4,04 để tính t. Lời giải chi tiết :
a) Vào năm 2023, t = 2023 – 2000 = 23 Diện tích rừng Sác được phủ xanh vào năm 2023 là: \(S = 3,14 + 0,05.23 = 4,29\) (nghìn ha) b) Diện tích rừng Sác được phủ xanh đạt 4,04 nghìn hécta khi: \(\begin{array}{l}3,14 + 0,05.t = 4,04\\ \Rightarrow t = \frac{{4,04 - 3,14}}{{0,05}} = 18\end{array}\) Khi đó là năm 2000 + 18 = 2018. Phương pháp giải :
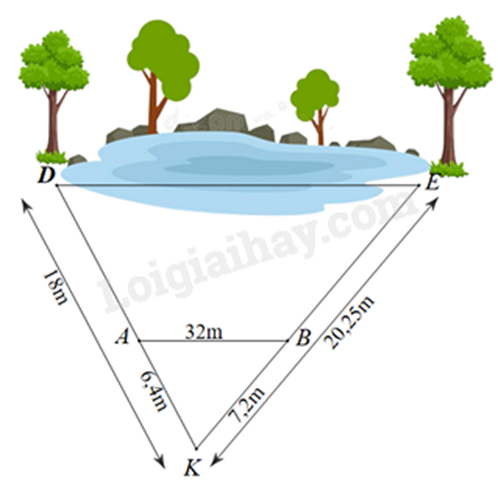
a) Dựa vào tỉ số hai đoạn thẳng để chứng minh. b) Dựa vào định lí Thales đảo để chứng minh. c) Áp dụng hệ quả của định lí Thales để suy ra tỉ số giữa AB và DE để tính DE. Lời giải chi tiết :
a) Ta có: \(\begin{array}{l}\frac{{KB}}{{KE}} = \frac{{7,2}}{{20,25}} = \frac{{16}}{{45}}\\\frac{{KA}}{{KD}} = \frac{{6,4}}{{18}} = \frac{{16}}{{45}}\end{array}\) suy ra \( \frac{{KB}}{{KE}} = \frac{{KA}}{{KD}}\) (đpcm) b) Vì \(\frac{{KB}}{{KE}} = \frac{{KA}}{{KD}}\) (cmt) nên AB // DE (Định lí Thales đảo trong tam giác) c) Vì AB // DE nên ta có: \(\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{KA}}{{KD}} = \frac{{16}}{{45}}\\\frac{{32}}{{DE}} = \frac{{16}}{{45}}\\ DE = 32:\frac{{16}}{{45}} = 90\left( m \right)\end{array}\) Vậy khoảng cách giữa D và E là 90m. Phương pháp giải :
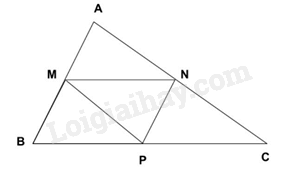
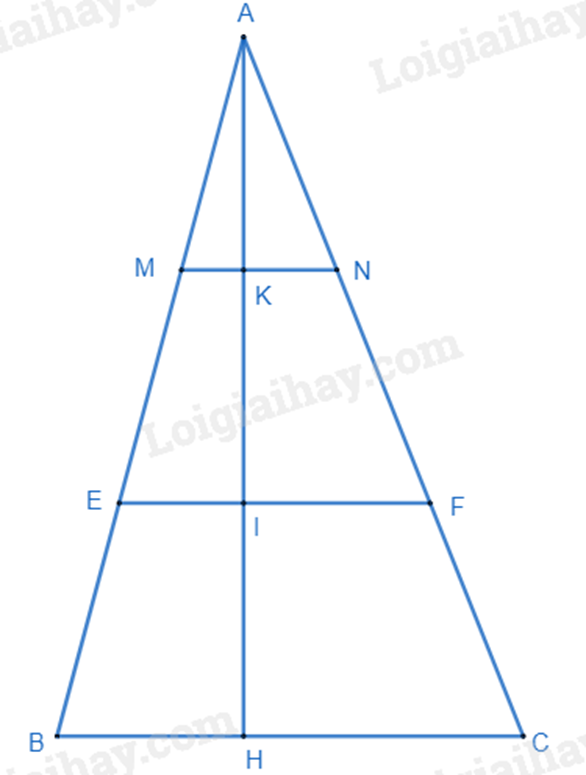
a) Áp dụng hệ quả của định lí Thales để suy ra tỉ số giữa MN, EF với BC. b) Tính độ dài AH qua công thức tính diện tích tam giác. Từ đó suy ra AK. Chứng minh MNFE là hình thang, KI là đường cao của hình thang MNFE. Sử dụng công thức tính diện tích hình thang. Lời giải chi tiết :
a) Theo bài ra ta có \(AK = KI = IH\)\( \Rightarrow \frac{{AK}}{{AH}} = \frac{1}{3};\frac{{AI}}{{AH}} = \frac{2}{3}\). Áp dụng hệ quả của định lí Thales vào tam giác ABH có MK // BH và EI // BH \( \Rightarrow \frac{{MK}}{{BH}} = \frac{{AK}}{{AH}} = \frac{1}{3}\); \(\frac{{EI}}{{BH}} = \frac{{AI}}{{AH}} = \frac{2}{3}\) (1) Áp dụng hệ quả của định lí Thales vào tam giác ACH có NK // CH và FI // CH \( \Rightarrow \frac{{NK}}{{CH}} = \frac{{AK}}{{AH}} = \frac{1}{3}\); \(\frac{{FI}}{{CH}} = \frac{{AI}}{{AH}} = \frac{2}{3}\) (2) Từ (1) và (2), áp dụng dãy tỉ số bằng nhau ta có: \(\frac{{MK}}{{BH}} = \frac{{NK}}{{CH}} = \frac{{MK + NK}}{{BH + CH}} = \frac{{MN}}{{BC}} = \frac{1}{3}\)\( \Rightarrow MN = \frac{1}{3}BC = \frac{{20}}{3}\left( {cm} \right)\) \(\frac{{EI}}{{BH}} = \frac{{FI}}{{CH}} = \frac{{EI + FI}}{{BH + CH}} = \frac{{EF}}{{BC}} = \frac{2}{3}\)\( \Rightarrow EF = \frac{2}{3}BC = \frac{2}{3}.20 = \frac{{40}}{3}\left( {cm} \right)\) b) Diện tích tam giác ABC là \(300c{m^2}\) \(\begin{array}{l} \Rightarrow \frac{1}{2}AH.BC = 300\\\frac{1}{2}AH.20 = 300\\ \Rightarrow AH = 300:\frac{{20}}{2} = 30\left( {cm} \right)\end{array}\) Ta có: \(\frac{{AK}}{{AH}} = \frac{1}{3} \Rightarrow AK = \frac{1}{3}AH = \frac{1}{3}.30 = 10\left( {cm} \right)\) \( \Rightarrow \) KI = AK = 10 cm. Vì MN và EF cùng song song với BC nên MNFE là hình thang. Vì \(AH \bot BC \Rightarrow AH \bot MN\) và \(AH \bot EF\) \( \Rightarrow KI\) là đường cao của hình thang MNFE \(\left( {K \in MN;I \in EF} \right)\). Diện tích hình thang MNFE là: \({S_{MNFE}} = \frac{1}{2}\left( {MN + EF} \right).KI = \frac{1}{2}.\left( {\frac{{20}}{3} + \frac{{40}}{3}} \right).10 = 100\left( {c{m^2}} \right)\) Vậy \({S_{MNFE}} = 100c{m^2}\). Phương pháp giải :
- Tìm tọa độ giao điểm của đường thẳng với các trục tọa độ. - Sử dụng công thức tính diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông. - Giải phương trình để tìm m. Lời giải chi tiết :
Ta có: \(d \cap Oy = \left\{ B \right\} \Rightarrow {x_B} = 0 \Rightarrow {y_B} = - 1\)\( \Rightarrow B\left( {0; - 1} \right) \Rightarrow OB = \left| { - 1} \right| = 1\). \(d \cap Ox = \left\{ A \right\} \Rightarrow {y_A} = 0\)\( \Rightarrow \left( {2m + 1} \right){x_A} - 1 = 0 \Rightarrow {x_A} = \frac{1}{{2m + 1}}\left( {m \ne \frac{{ - 1}}{2}} \right)\)\( \Rightarrow A\left( {\frac{1}{{2m + 1}};0} \right) \Rightarrow OA = \left| {\frac{1}{{2m + 1}}} \right|\). Theo bài ra ta có: \({S_{\Delta AOB}} = \frac{1}{2}OA.OB = \frac{1}{2}\) \(\frac{1}{2}.1.\left| {\frac{1}{{2m + 1}}} \right| = \frac{1}{2}\) \(\left| {\frac{1}{{2m + 1}}} \right| = 1\) \(\left| {2m + 1} \right| = 1\) \(\left[ \begin{array}{l}m = 0\\m = 1\end{array} \right.\) (tmđk) Vậy \(m \in \left\{ { - 1;0} \right\}\) thì d cắt 2 trục tọa độ tạo thành tam giác có diện tích bằng \(\frac{1}{2}\).
|