Đề thi, đề kiểm tra Toán lớp 8 - Chân trời sáng tạo

Đề thi giữa kì 2 Toán 8 - Đề số 8 - Chân trời sáng tạo

Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên

Tải về

Làm đề thi

Phần trắc nghiệm (2 điểm) Câu 1: Chọn khẳng định sai. A. $y = 6x + 8$ có hệ số của $x$ là 6 ; hệ số tự do là 8 .

Đề bài

I. Trắc nghiệm

Câu 1 :

Chọn khẳng định sai.

A
$y = 6x + 8$ có hệ số của $x$ là 6 ; hệ số tự do là 8 .
B
$y = - x - 5$ có hệ số của $x$ là -1 ; hệ số tự do là -5 .
C
$y = \frac{x}{3}$ có hệ số của $x$ là $\frac{1}{3}$ ; hệ số tự do là 1 .
D
$y = 2 - 2x$ có hệ số của $x$ là -2 , hệ số tự do là 2.

Câu 2 :

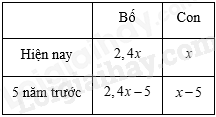
Tuổi bố hiện nay gấp 2,4 lần tuổi con. 5 năm trước đây, tuổi bố gấp $\frac{{11}}{4}$ lần tuổi con. Tính tuổi con hiện nay.

A
25 tuổi
B
60 tuổi
C
35 tuổi
D
10 tuổi

Câu 3 :

Với $x = 7$ là nghiệm của phương trình nào dưới đây?

A
$11 - 2x = x - 1$
B
$5x + 14 = - 2x$
C
$x - 9 = 5 - x$
D
$3x + 1 = 7x - 11$

Câu 4 :

Hai đường thẳng $y = - 5x$ và $y = - 5x + 2$

A
trùng nhau
B
song song
C
vuông góc
D
cắt nhau

Câu 5 :

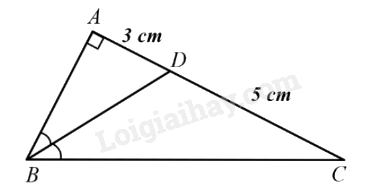
Cho tam giác ${\rm{ABC}}$ vuông tại $A$ và có đường phân giác $BD\left( {D \in AC} \right)$ . Biết $AD = 3{\rm{\;cm}},DC = 5{\rm{\;cm}}$ . Tính độ dài các đoạn thẳng ${\rm{BC}}$ .

A
$8{\rm{\;cm}}$
B
$13{\rm{\;cm}}$
C
$15{\rm{\;cm}}$
D
$10{\rm{\;cm}}$

Câu 6 :

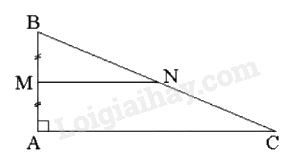
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5{\rm{\;cm}}$ và $BC = 13{\rm{\;cm}}$ . Qua trung điểm $M$ của ${\rm{AB}}$ , vẽ một đường thẳng song song với ${\rm{AC}}$ cắt ${\rm{BC}}$ tại ${\rm{N}}$ . Tính độ dài ${\rm{MN}}$ .

A
$6\left( {{\rm{\;m}}} \right)$
B
$7,5\left( {{\rm{\;m}}} \right)$
C
$2,5\left( {{\rm{\;m}}} \right)$
D
$10\left( {{\rm{\;m}}} \right)$

Câu 7 :

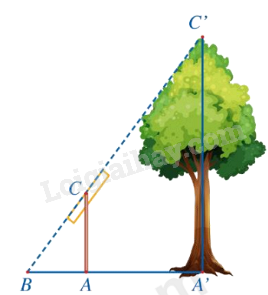
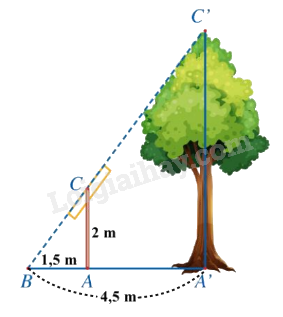
Trong hình dưới đây, độ dài đoạn thẳng ${\rm{A'C'}}$ mô tả chiều cao của một cái cây, đoạn thẳng ${\rm{AC}}$ mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm $\left. {A',A,B} \right)$ . Giả sử $AC = 2{\rm{\;m}},AB = 1,5{\rm{\;m}},A'B = 4,5{\rm{\;m}}$ . Tính chiều cao của cây.

A
$6{\rm{\;m}}$
B
$1,5{\rm{\;m}}$
C
$7{\rm{\;m}}$
D
$5{\rm{\;m}}$

Câu 8 :

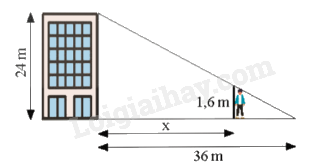
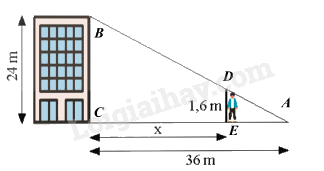
Một toà nhà cao $24{\rm{\;m}}$ , đổ bóng nắng dài $36{\rm{\;m}}$ trên đường như hình sau. Một người cao 1,6 m muốn đứng trong bóng râm của toà nhà. Hỏi người đó có thể đứng cách toà nhà xa nhất bao nhiêu mét?

A
$36,3{\rm{\;m}}$
B
$33,6{\rm{\;m}}$
C
$36{\rm{\;m}}$
D
$36,6{\rm{\;m}}$

II. Tự luận

Câu 1 :

Tìm hệ số góc của mỗi đường thẳng sau:
a) $y = - 1,7x - 1,7$ ;
b) $y = - \sqrt 5 x + 1$ ;
c) $y = \frac{9}{{ - 11}}x + \frac{{15}}{8}$
d) $y = \frac{1}{{\sqrt 3 }}x - \sqrt {11}$ .

Câu 2 :

Giải các phương trình:
a) $\frac{{2x}}{{15}} - \frac{{15 - 2x}}{{10}} = \frac{7}{6}$ ;
b) $\frac{x}{{20}} - \frac{{x + 10}}{{25}} = 2$ ;
c) $\frac{{2x - 37}}{3} = - 4x + 5$ ;
d) $\frac{{3\left( {3x + 1} \right) + 2}}{2} - 3 = \frac{{2\left( {5x + 1} \right)}}{3} - \frac{{3x + 1}}{6}$

Câu 3 :

Giá niêm yết của một máy lọc nước và một nồi cơm điện có tổng là 6,5 triệu đồng. Bác Bình mua hàng vào đúng dịp tri ân khách hàng nên so với giá niêm yết máy lọc nước được giảm giá $15{\rm{\% }}$ và nồi cơm điện được giảm giá $10{\rm{\% }}$ . Do đó, tổng số tiền bác phải trả là 5,65 triệu đồng. Tính giá tiền niêm yết của mỗi sản phẩm đã nêu.

Câu 4 :

Hiện tại, cô Hạnh đã tiết kiệm được 500 triệu đồng. Để thực hiện dự định mua một căn chung cư có giá trị 2,6 tỉ đồng, cô Hạnh đã lên kế hoạch hằng tháng tiết kiệm 15 triệu đồng. Gọi y (triệu đồng) là số tiền cô Hạnh tiết kiệm được sau $x$ (tháng) kể từ hiện tại.

a) Viết công thức tính $y$ theo $x$ . Hỏi $y$ có phải là hàm số bậc nhất của $x$ hay không?

b) Hỏi sau bao lâu kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm?

Câu 5 :

Cho tam giác ${\rm{ABC}}$ vuông tại $A(AB < AC)$ , kẻ đường cao ${\rm{AH}}$ , đường trung tuyến ${\rm{AM}}$ . Đường thẳng vuông góc với ${\rm{AM}}$ tại $A$ cắt đường thẳng ${\rm{BC}}$ tại $D$ . Chứng minh rằng:
a) ${\rm{AB}}$ là tia phân giác của $\widehat {DAH}$ .
b) $BH.CD = BD.CH$ .

Lời giải và đáp án

I. Trắc nghiệm

Câu 1 :

Chọn khẳng định sai.

A
$y = 6x + 8$ có hệ số của $x$ là 6 ; hệ số tự do là 8 .
B
$y = - x - 5$ có hệ số của $x$ là -1 ; hệ số tự do là -5 .
C
$y = \frac{x}{3}$ có hệ số của $x$ là $\frac{1}{3}$ ; hệ số tự do là 1 .
D
$y = 2 - 2x$ có hệ số của $x$ là -2 , hệ số tự do là 2.

Đáp án : C

Phương pháp giải :

Hàm số bậc nhất có dạng $y = ax + b\left( {a \ne 0} \right)$ với a là hệ số của $x$ , b là hệ số tự do

Lời giải chi tiết :

$y = 6x + 8$ có hệ số của $x$ là 6 ; hệ số tự do là 8

$y = - x - 5$ có hệ số của $x$ là -1 ; hệ số tự do là -5

$y = \frac{x}{3}$ có hệ số của $x$ là $\frac{1}{3}$ ; hệ số tự do là 0

$y = 2 - 2x$ có hệ số của $x$ là -2 , hệ số tự do là 2

Đáp án C.

Câu 2 :

Tuổi bố hiện nay gấp 2,4 lần tuổi con. 5 năm trước đây, tuổi bố gấp $\frac{{11}}{4}$ lần tuổi con. Tính tuổi con hiện nay.

A
25 tuổi
B
60 tuổi
C
35 tuổi
D
10 tuổi

Đáp án : A

Phương pháp giải :

Giải bài toán bằng cách lập phương trình bậc nhất.

PT: 5 năm trước tuổi bố gấp $\frac{{11}}{4}$ lần tuổi con

Lời giải chi tiết :

Gọi tuổi con hiện nay là $x(x \in N,x > 5)$ .

Tuổi bố hiện nay là 2,4x.

Do đó, 5 năm trước tuổi con là $x - 5$ , tuổi bố là $2,4x - 5$ .

Ta có phương trình:

$2,4x - 5 = \frac{{11}}{4}\left( {x - 5} \right)$

$2,4x - 5 = 2,75x - 13,75$

$2,75x - 2,4x = 13,75 - 5$

$0,35x = 8,75$

$x = 25\left( {TM} \right)$

Vậy hiện nay tuổi con là 25 tuổi.

Đáp án A.

Câu 3 :

Với $x = 7$ là nghiệm của phương trình nào dưới đây?

A
$11 - 2x = x - 1$
B
$5x + 14 = - 2x$
C
$x - 9 = 5 - x$
D
$3x + 1 = 7x - 11$

Đáp án : A

Phương pháp giải :

Nếu hai vế của phương trình (ẩn $x$ ) nhận cùng một giá trị khi $x = a$ thì số $a$ gọi là một nghiệm của phương trình đó.

Lời giải chi tiết :

Với $x = 7$ :

Xét $11 - 2x = x - 1$ có: $VT = 11 - 2.7 = 11 - 14 = - 3;VP = 7 - 1 = 6$

$\Rightarrow VT \ne VP \Rightarrow x = 7$ không là nghiệm của phương trình.

Xét $5x + 14 = - 2x$ có: $VT = 5.7 + 14 = 28;VP = - 2.7 = - 14$

$\Rightarrow VT \ne VP \Rightarrow x = 7$ không là nghiệm của phương trình.

Xét $x - 9 = 5 - x$ có: $VT = 7 - 9 = - 2;VP = 5 - 7 = - 2$

$\Rightarrow VT = VP \Rightarrow x = 7$ là nghiệm của phương trình.

Xét $3x + 1 = 7x - 11$ có: $VT = 3.7 + 1 = 22;VP = 7.7 - 11 = 38$

$\Rightarrow VT \ne VP \Rightarrow x = 7$ không là nghiệm của phương trình.

Đáp án A.

Câu 4 :

Hai đường thẳng $y = - 5x$ và $y = - 5x + 2$

A
trùng nhau
B
song song
C
vuông góc
D
cắt nhau

Đáp án : B

Phương pháp giải :

Cho hai đường thẳng $d:y = ax + b\left( {a \ne 0} \right)$ và $d':y = a'x + b'\left( {a' \ne 0} \right)$ nếu $a = a';b \ne b'$ thì ${\rm{d}}\parallel {\rm{d'}}$

Lời giải chi tiết :

Xét $y = - 5x + 0$ và $y = - 5x + 2$ có: $\left\{ {\begin{array}{*{20}{l}}{ - 5 = - 5}\\{0 \ne 2}\end{array}} \right.$ suy ra $d\parallel d'$

Đáp án B.

Câu 5 :

A
$8{\rm{\;cm}}$
B
$13{\rm{\;cm}}$
C
$15{\rm{\;cm}}$
D
$10{\rm{\;cm}}$

Đáp án : D

Phương pháp giải :

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

Áp dụng Pythagore trong $\Delta ABC$ vuông tại $A$ .

Lời giải chi tiết :

$\Delta ABC$ có $BD$ là tia phân giác của góc B suy ra $\frac{{AB}}{{BC}} = \frac{{AD}}{{DC}} = \frac{3}{5}$ hay $\frac{{AB}}{3} = \frac{{BC}}{5} = k(k \in \mathbb{R},k > 0)$ .

Suy ra: $AB = 3k,BC = 5k$ .

Áp dụng định lí Pythagore trong $\Delta ABC$ vuông tại $A$ ta có:

$B{C^2} = A{B^2} + A{C^2}$ hay ${(5k)^2} = {(3k)^2} + {(5 + 3)^2}$ , suy ra $k = 2$

Từ đó ta có: $BC = 10{\rm{\;cm}}$ .

Đáp án D.

Câu 6 :

A
$6\left( {{\rm{\;m}}} \right)$
B
$7,5\left( {{\rm{\;m}}} \right)$
C
$2,5\left( {{\rm{\;m}}} \right)$
D
$10\left( {{\rm{\;m}}} \right)$

Đáp án : A

Phương pháp giải :

Áp dụng định lí Pythagore vào $\Delta {\rm{ABC}}$ vuông tại ${\rm{A}}$ để tính cạnh ${\rm{AC}}$ .

Áp dụng định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Từ đó suy ra ${\rm{MN}}$ là đường trung bình.

Đường trung bình của tam giác thì song song vơi cạnh thứ ba và bằng nửa cạnh ấy.

Lời giải chi tiết :

Áp dụng định lí Pythagore vào $\Delta {\rm{ABC}}$ vuông tại ${\rm{A}}$ có: ${\rm{B}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2}$ hay ${\rm{A}}{{\rm{C}}^2} = {\rm{B}}{{\rm{C}}^2} - {\rm{A}}{{\rm{B}}^2} = {13^2} - {5^2} = 144$ suy ra ${\rm{AC}} = 12{\rm{\;cm}}$

Xét $\Delta {\rm{ABC}}$ có ${\rm{MA}} = {\rm{MB}}$ (theo gt); ${\rm{MN}}//{\rm{AC}}$ (theo gt) nên ${\rm{NB}} = {\rm{NC}}$

Do đó ${\rm{MN}}$ là đường trung bình của $\Delta {\rm{ABC}}$ suy ra ${\rm{MN}} = \frac{1}{2}{\rm{AC}}$ hay ${\rm{MN}} = \frac{1}{2} \cdot 12 = 6\left( {{\rm{\;cm}}} \right)$ .

Đáp án A.

Câu 7 :

A
$6{\rm{\;m}}$
B
$1,5{\rm{\;m}}$
C
$7{\rm{\;m}}$
D
$5{\rm{\;m}}$

Đáp án : A

Phương pháp giải :

Áp dụng hệ quả định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Lời giải chi tiết :

Ta có $\left. {\begin{array}{*{20}{c}}{AC \bot A'B}\\{A'C' \bot A'B}\end{array}} \right\}$ nên $AC\parallel A'C'$

Xét $\Delta ABA'$ với $AC\parallel A'C'$ có: $\frac{{AC}}{{A'C'}} = \frac{{BA}}{{BA'}}$ (Hệ quả của định lí Thales) hay $\frac{2}{{A'C'}} = \frac{{1,5}}{{4,5}}$ suy ra $A'C' = \frac{{2.4,5}}{{1,5}} = 6\left( {{\rm{\;m}}} \right)$

Vậy cây cao 6m.

Đáp án A.

Câu 8 :

A
$36,3{\rm{\;m}}$
B
$33,6{\rm{\;m}}$
C
$36{\rm{\;m}}$
D
$36,6{\rm{\;m}}$

Đáp án : B

Phương pháp giải :

Dựng các điểm lên hình vẽ.

Áp dụng hệ quả định lí Thales: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ vơi ba cạnh của tam giác đã cho.

Lời giải chi tiết :

Xét $\Delta ABC$ có $DE//BC$ nên theo hệ quả của định lí Thales ta có:

$\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AC - CE}}{{AC}}$ hay $\frac{{1,6}}{{24}} = \frac{{36 - x}}{{36}}$

Suy ra $36 - x = \frac{{1,6.36}}{{24}}$ hay $x = 36 - \frac{{1,6.36}}{{24}} = 33,6$

Vậy người đó có thể đứng xa tòa nhà nhất là $33,6{\rm{\;m}}$ .

Đáp án B.

II. Tự luận

Câu 1 :

Tìm hệ số góc của mỗi đường thẳng sau:
a) $y = - 1,7x - 1,7$ ;
b) $y = - \sqrt 5 x + 1$ ;
c) $y = \frac{9}{{ - 11}}x + \frac{{15}}{8}$
d) $y = \frac{1}{{\sqrt 3 }}x - \sqrt {11}$ .

Phương pháp giải :

Hệ số $a$ gọi là hệ số góc của đường thẳng $y = ax + b\left( {a \ne 0} \right)$ .

Lời giải chi tiết :

Hệ số góc của các đường thẳng $y = - 1,7x - 1,7$ là: $- 1,7$ ;

Hệ số góc của các đường thẳng $y = - \sqrt 5 x + 1$ là: $- \sqrt 5$ ;

Hệ số góc của các đường thẳng $y = \frac{9}{{ - 11}}x + \frac{{15}}{8}$ là: $\frac{9}{{ - 11}}$ ;

Hệ số góc của các đường thẳng $y = \frac{1}{{\sqrt 3 }}x - \sqrt {11}$ là: $\frac{1}{{\sqrt 3 }}$

Câu 2 :

Phương pháp giải :

Chuyển các số hạng chứa ẩn sang một vế.

Chuyển các hằng số sang vế còn lại.

Lời giải chi tiết :

a) $\frac{{2x}}{{15}} - \frac{{15 - 2x}}{{10}} = \frac{7}{6}$

$\frac{{4x}}{{30}} - \frac{{45 - 6x}}{{30}} = \frac{{35}}{{30}}$

$4x - 45 + 6x = 35$

$4x + 6x = 35 + 45$

$10x = 80$

$x = 8$

Vậy $x = 8$

b) $\frac{x}{{20}} - \frac{{x + 10}}{{25}} = 2$

$\frac{{5x}}{{100}} - \frac{{4x + 40}}{{100}} = \frac{{200}}{{100}}$

$5x - 4x - 40 = 200$

$x = 200 + 40$

$x = 240$

Vậy $x = 240$

c) $\frac{{2x - 37}}{3} = - 4x + 5$

$2x - 37 = 3\left( { - 4x + 5} \right)$

$2x - 37 = - 12x + 15$

$2x + 12x = 15 + 37$

$14x = 52$

$x = \frac{{26}}{7}$

Vậy $x = \frac{{26}}{7}$

d) $\frac{{3\left( {3x + 1} \right) + 2}}{2} - 3 = \frac{{2\left( {5x + 1} \right)}}{3} - \frac{{3x + 1}}{6}$

$\frac{{9\left( {3x + 1} \right) + 6}}{6} - \frac{{18}}{6} = \frac{{4\left( {5x + 1} \right)}}{6} - \frac{{3x + 1}}{6}$

$27x + 9 + 6 - 18 = 20x + 4 - 3x - 1$

$27x - 20x + 3x = 4 - 1 + 18 - 9$

$10x = 12$

$x = \frac{6}{5}$

Vậy $x = \frac{6}{5}$

Câu 3 :

Phương pháp giải :

Giải bài toán bằng cách lập phương trình bậc nhất.

PT: tổng giá tiền lúc sau là 6,5 triệu đồng.

Lời giải chi tiết :

Gọi giá niêm yết của máy lọc nước là $x$ (triệu đồng). Điều kiện $x < 6,5$

Giá niêm yết của nồi cơm điện là $6,5 - x$ (triệu đồng)

Giá sau khi giảm của máy lọc nước là $\left( {100{\rm{\% }} - 15{\rm{\% }}} \right) \cdot x = 0,85x$ (triệu đồng)

Giá sau khi giảm của nồi cơm điện là $\left( {100{\rm{\% }} - 10{\rm{\% }}} \right).\left( {6,5 - x} \right) = 0,9.\left( {6,5 - x} \right)$

Theo giả thiết, ta có phương trình:

$0,85x + 0,9 \cdot \left( {6,5 - x} \right) = 5,65$

$0,85x + 5,85 - 0,9x = 5,65$

$- 0,05x + 5,85 = 5,65$

$- 0,05x = 5,65 - 5,85$

$- 0,05x = - 0,2$

$x = \left( { - 0,2} \right):\left( { - 0,05} \right)$

$x = 4\left( {TM} \right)$

Vậy giá niêm yết của mày lọc nước là 4 triệu đồng và giá niêm yết của nồi cơm điện là 2,5 triệu đồng.

Câu 4 :

a) Viết công thức tính $y$ theo $x$ . Hỏi $y$ có phải là hàm số bậc nhất của $x$ hay không?

b) Hỏi sau bao lâu kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm?

Phương pháp giải :

a) Hàm số bậc nhất có dạng $y = ax + b$ , trong đó ${\rm{a}},{\rm{b}}$ là các số cho trước và a khác 0 .

b) Dựa vào dữ kiện đề bài cho để thay giá trị cho đúng.

Lời giải chi tiết :

a) Ta có: $y = 15x + 500$ .

Vậy $y$ là hàm số bậc nhất của $x$ .

b) Ta có: $15x + 500 = 2600$ suy ra $x = 140$ .

Mà 140 tháng $= 11$ năm +8 tháng, suy ra sau 11 năm 8 tháng kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm.

Câu 5 :

Phương pháp giải :

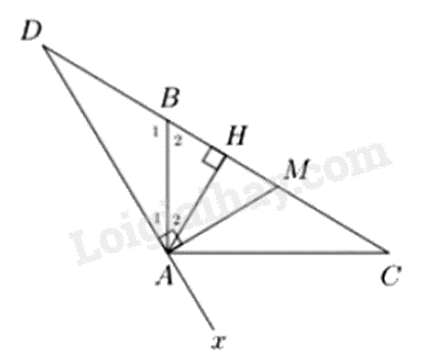
a) Chứng minh bắc cầu: $\left\{ {\begin{array}{*{20}{l}}{\widehat {DAB} + \widehat {BAM} = \widehat {DAM} = {{90}^0}\left( {do\,AM \bot AD} \right)}\\{\widehat {BAH} + \widehat {ABH} = \widehat {AHB} = {{90}^0}\left( {do\,AH \bot BC} \right)}\end{array}} \right.$

Chứng minh được: $\widehat {MBA} = \widehat {MAB}$

suy ra $\widehat {DAB} = \widehat {BAH}$ (cùng phụ với hai góc bằng nhau)

b) Sử dụng tính chất đường phân giác trong ${\rm{AB}}$ của tam giác ${\rm{ADH}}$

Sử dụng tính chất đường phân giác ngoài ${\rm{AC}}$ tại đỉnh ${\rm{A}}$ của tam giác ${\rm{ADH}}$ .

Lời giải chi tiết :

a) $\Delta ABC$ vuông tại $A$ , đường trung tuyến $AM$ nên $AM = MB$ suy ra $\Delta AMB$ cân tại $M$

suy ra $\widehat {MBA} = \widehat {MAB}$ hay $\widehat {BAM} = \widehat {ABH}$

Ta có: $\left\{ {\begin{array}{*{20}{l}}{\widehat {DAB} + \widehat {BAM} = \widehat {DAM} = {{90}^0}\left( {do\,AM \bot AD} \right)}\\{\widehat {BAH} + \widehat {ABH} = \widehat {AHB} = {{90}^0}\left( {do\,AH \bot BC} \right)}\end{array}} \right.$

suy ra $\widehat {DAB} = \widehat {BAH}$ (cùng phụ với hai góc bằng nhau)

suy ra $AB$ là tia phân giác của $\widehat {DAH}$ .

b) Vì $AB$ là tia phân giác của $\widehat {DAH}$ nên $\frac{{BH}}{{BD}} = \frac{{AH}}{{AD}}$ (tính chất đường phân giác)

Vì $AC \bot AB,\widehat {DAH}$ kề bù với $\widehat {HAx}$ nên $AC$ là tia phân giác $\widehat {HAx}$ suy ra $\frac{{CH}}{{CD}} = \frac{{AH}}{{AD}}$

Suy ra $\frac{{BH}}{{BD}} = \frac{{AH}}{{AD}} = \frac{{CH}}{{CD}}$ . Do đó $BH \cdot CD = CH \cdot BD$ .

Bài liên quan

Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9

Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 10

Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề thi giữa kì 2 Toán 8 - Đề số 7 - Chân trời sáng tạo

Phần trắc nghiệm (2 điểm) Câu 1: Đường trung bình của tam giác: A. Là đoạn thẳng nối hai điểm bất kì trên hai cạnh của tam giác
Đề thi giữa kì 2 Toán 8 - Đề số 6 - Chân trời sáng tạo

Phần trắc nghiệm (2 điểm) Câu 1: Cho tam giác ${\rm{ABC}}$ có $AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}$ . Các điểm ${\rm{M}},{\rm{N}}$ lần lượt thuộc các cạnh ${\rm{AB}},{\rm{AC}}$ thoả mãn $AM = 3{\rm{\;cm}}$ và $MN\parallel BC$ . Tính độ dài đoạn thẳng ${\rm{AN}}$ .
Đề thi giữa kì 2 Toán 8 - Đề số 5 - Chân trời sáng tạo

Phần trắc nghiệm (3 điểm) Câu 1 (150991): Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?