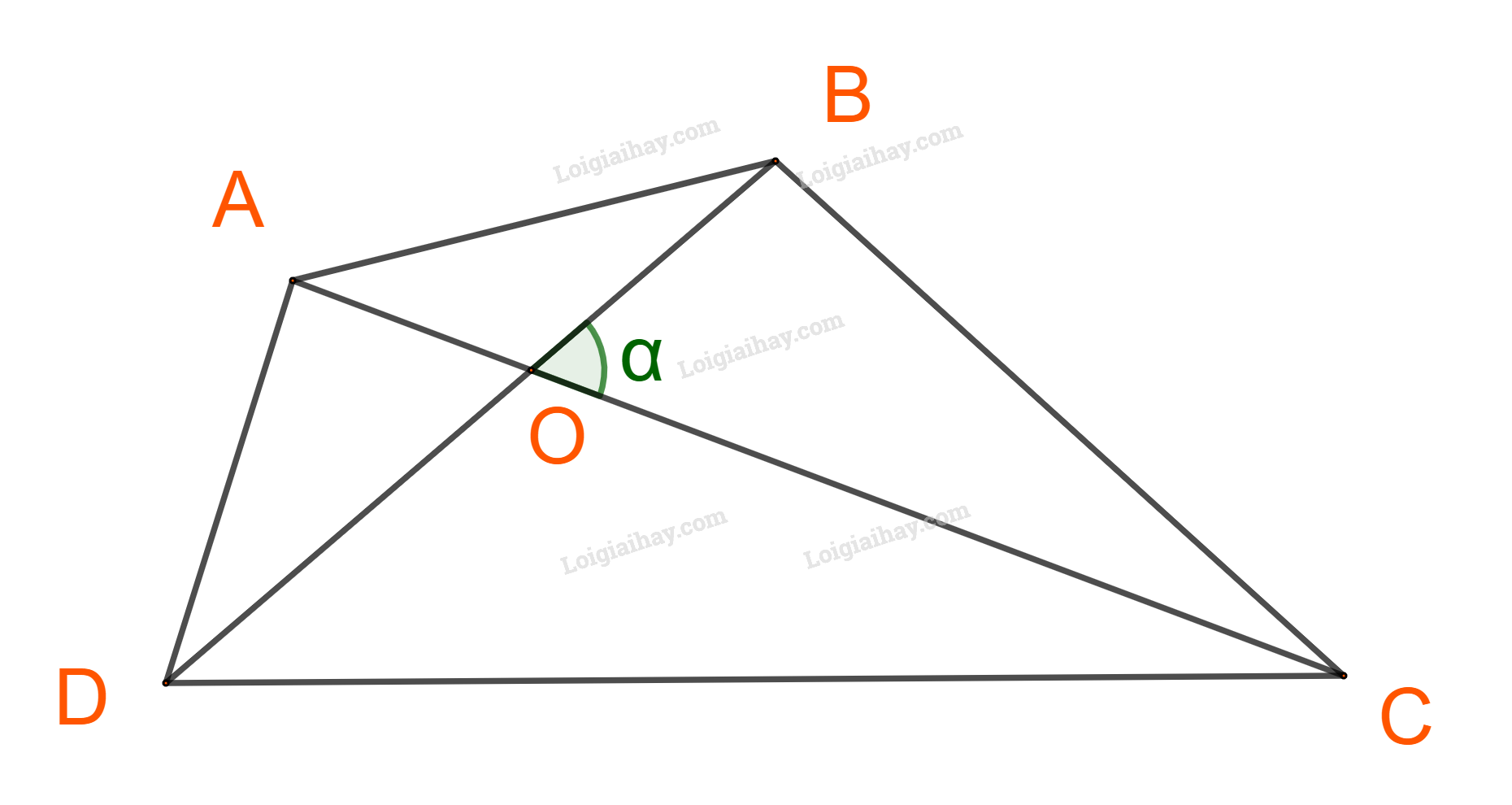
Giải bài 10 trang 73 SGK Toán 10 tập 1 – Chân trời sáng tạo

Đề bài

Cho tứ giác lồi ABCD có các đường chéo $AC = x,BD = y$ và góc giữa AC và BD bằng $\alpha .$ Gọi S là diện tích của tứ giác ABCD.

a) Chứng minh $S = \frac{1}{2}xy.\sin \alpha$

b) Nêu kết quả trong trường hợp $AC \bot BD.$

Lời giải chi tiết

Gọi O là giao điểm của AC và BD.

a) Áp dụng công thức $S = \frac{1}{2}ac.\sin B$, ta có:

$\begin{array}{l}{S_{OAD}} = \frac{1}{2}.OA.OD.\sin \alpha ;\quad {S_{OBC}} = \frac{1}{2}.OB.OC.\sin \alpha ;\\{S_{OAB}} = \frac{1}{2}.OA.OB.\sin ({180^o} - \alpha );\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin ({180^o} - \alpha ).\end{array}$

Mà $\sin ({180^o} - \alpha ) = \sin \alpha$

$\Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB.\sin \alpha ;\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin \alpha .$

$\begin{array}{l} \Rightarrow {S_{ABCD}} = \left( {{S_{OAD}} + {S_{OAB}}} \right) + \left( {{S_{OBC}} + {S_{OCD}}} \right)\\ = \frac{1}{2}.OA.\sin \alpha .(OD + OB) + \frac{1}{2}.OC.\sin \alpha .(OB + OD)\\ = \frac{1}{2}.OA.\sin \alpha .BD + \frac{1}{2}.OC.\sin \alpha .BD\\ = \frac{1}{2}.BD.\sin \alpha .(OA + OC)\\ = \frac{1}{2}.AC.BD.\sin \alpha  = \frac{1}{2}.x.y.\sin \alpha .\end{array}$

b) Nếu $AC \bot BD$ thì $\alpha  = {90^o} \Rightarrow \sin \alpha  = 1.$

$\Rightarrow {S_{ABCD}} = \frac{1}{2}.x.y.1 = \frac{1}{2}.x.y.$