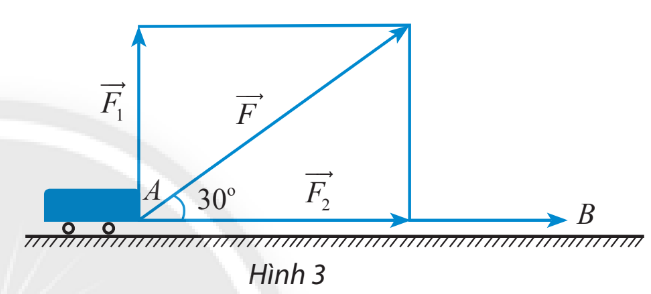
Giải bài 11 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo

Đề bài

Một xe goòng được kéo bởi một lực $\overrightarrow F$ có độ lớn là là 50 N, di chuyển theo quãng đường từ A đến B có chiều dài là 200 m. Cho biết góc giữa lực $\overrightarrow F$ và $\overrightarrow {AB}$ là $30^\circ$ và  $\overrightarrow F$ được phân tích thành 2 lực $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}}$ (hình 3). Tính công sinh ra bởi các lực $\overrightarrow F ,\overrightarrow {{F_1}}$ và $\overrightarrow {{F_2}}$.

Lời giải chi tiết

Ta xác định được các độ lớn:

$\left| {\overrightarrow F } \right| = 50,\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow F } \right|\cos 30^\circ  = 50.\frac{{\sqrt 3 }}{2} = 25\sqrt 3 ,\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow F } \right|.\sin 30^\circ  = 50.\frac{1}{2} = 25$ (N)

Dựa vào hình vẽ ta có: $\left( {\overrightarrow F ,\overrightarrow d } \right) = 30^\circ ,\left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 90^\circ ,\left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 0^\circ$

Áp dụng công thức tính công sinh ra bởi lực $A = \overrightarrow F .\overrightarrow d$ ta có:

$A = \overrightarrow F .\overrightarrow d  = \left| {\overrightarrow F } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 50.200.\cos 30^\circ  = 5000\sqrt 3 (J)$

${A_1} = \overrightarrow {{F_1}} .\overrightarrow d  = \left| {\overrightarrow {{F_1}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 25.200.\cos 90^\circ  = 0 (J)$

${A_2} = \overrightarrow {{F_2}} .\overrightarrow d  = \left| {\overrightarrow {{F_2}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 25\sqrt 3 .200.\cos 0^\circ  = 5000\sqrt 3  (J)$