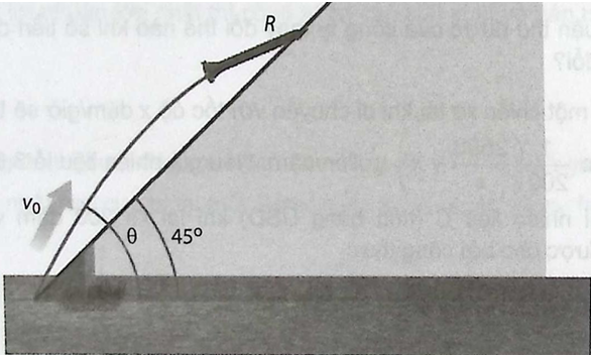
Giải bài 1.19 trang 16 sách bài tập toán 12 - Kết nối tri thứcMột vật được phóng lên trời theo một góc xiên (theta left( {{{45}^ circ } < theta < {{90}^ circ }} right)) so với phương ngang với vận tốc ban đầu là ({v_0}) (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc ({45^ circ }) so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet=0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số (Rleft( theta right) = frac{{v_0^2sqrt 2 }}{{16}}cos theta left( {si Đề bài Một vật được phóng lên trời theo một góc xiên \(\theta \left( {{{45}^ \circ } < \theta < {{90}^ \circ }} \right)\) so với phương ngang với vận tốc ban đầu là \({v_0}\) (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc \({45^ \circ }\) so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet=0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\) Góc ném \(\theta \) nào làm cho quãng đường R lớn nhất? Giá trị lớn nhất của R là bao nhiêu?
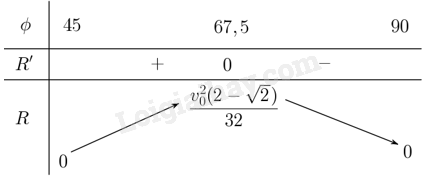
Phương pháp giải - Xem chi tiết Xét hàm số \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\). Yêu cầu bài toán tương đương tìm giá trị lớn nhất của hàm. Tính đạo hàm, lập bảng biến thiên của hàm số và đưa ra kết luận. Lời giải chi tiết Xét hàm số \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\). Ta cần tìm \(\theta \) để hàm số đạt giá trị lớn nhất. Ta có \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos \theta \sin \theta - {{\cos }^2}\theta } \right) = \frac{{v_0^2\sqrt 2 }}{{32}}\left( {2\cos \theta \sin \theta - 2{{\cos }^2}\theta } \right)\) \( = \frac{{v_0^2\sqrt 2 }}{{32}}\left( {\sin 2\theta - \cos 2\theta - 1} \right)\), \(\left( {{{45}^ \circ } < \theta < {{90}^ \circ }} \right)\). Do đó \(R' = \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos 2\theta + \sin 2\theta } \right)\). Khi đó \(R' = 0 \Leftrightarrow \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos 2\theta + \sin 2\theta } \right) = 0 \Leftrightarrow \cos 2\theta + \sin 2\theta = 0 \Leftrightarrow 2\theta = {135^ \circ } \Leftrightarrow \theta = {67,5^ \circ }\) (do \({45^ \circ } < \theta < {90^ \circ }\)). Mặt khác \(R\left( {{{45}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {45^ \circ }\left( {\sin {{45}^ \circ } - \cos {{45}^ \circ }} \right) = 0\); \(R\left( {{{67,5}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {67,5^ \circ }\left( {\sin {{67,5}^ \circ } - \cos {{67,5}^ \circ }} \right) = \frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}\); \(R\left( {{{90}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {90^ \circ }\left( {\sin {{90}^ \circ } - \cos {{90}^ \circ }} \right) = 0\). Lập bảng biến thiên của hàm số:
Từ bảng biến thiên suy ra hàm số đạt giá trị lớn nhất tại \(67,5\): \(\mathop {\max }\limits_{\left[ {45;90} \right]} R = R\left( {67,5} \right) = \frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}.\) Vậy khi góc ném \(\theta = {67,5^ \circ }\) thì quãng đường R là lớn nhất và bằng \(\frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}\) feet.
|