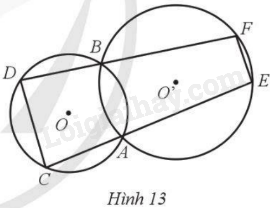
Giải bài 15 trang 90 sách bài tập toán 9 - Cánh diều tập 2Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A, B và CD là một dây cung của (O). Tia CA cắt (O’) tại E và tia DB cắt (O’) tại F. Chứng minh EF song song với CD. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.XYZ và nhận về những phần quà hấp dẫn Đề bài Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A, B và CD là một dây cung của (O). Tia CA cắt (O’) tại E và tia DB cắt (O’) tại F. Chứng minh EF song song với CD.
Phương pháp giải - Xem chi tiết Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng 180o. Lời giải chi tiết Ta có tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat {ACD} = \widehat {ABF}( = {180^o} - \widehat {ABD})\) (1). Mặt khác, tứ giác ABFE nội tiếp đường tròn (O’) suy ra \(\widehat {ABF} + \widehat {AEF} = {180^o}\) (2). Từ (1) và (2) ta có \(\widehat {ACD} + \widehat {AEF} = {180^o}\) hay \(\widehat {ECD} + \widehat {CEF} = {180^o}\). Suy ra EF // CD.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
|
