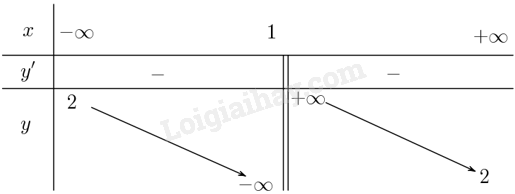
Giải bài 1.65 trang 36 sách bài tập toán 12 - Kết nối tri thứcCho hàm số (y = frac{{left( {m + 1} right)x - 2m + 1}}{{x - 1}}). a) Tìm (m) để tiệm cận ngang của đồ thị đi qua (left( {1;2} right)). b) Khảo sát và vẽ đồ thị (left( H right)) của hàm số (y = fleft( x right)) với (m) tìm được ở câu a. c) Từ đồ thị (left( H right)) của hàm số (y = fleft( x right)) ở câu b, vẽ đồ thị (y = left| {fleft( x right)} right|). Đề bài Cho hàm số \(y = \frac{{\left( {m + 1} \right)x - 2m + 1}}{{x - 1}}\). a) Tìm \(m\) để tiệm cận ngang của đồ thị đi qua \(\left( {1;2} \right)\). b) Khảo sát và vẽ đồ thị \(\left( H \right)\) của hàm số \(y = f\left( x \right)\) với \(m\) tìm được ở câu a. c) Từ đồ thị \(\left( H \right)\) của hàm số \(y = f\left( x \right)\) ở câu b, vẽ đồ thị \(y = \left| {f\left( x \right)} \right|\). Phương pháp giải - Xem chi tiết Ý a: Tìm tiệm cận ngang sau đó thay giá trị điểm \(\left( {1;2} \right)\) vào phương trình đường thẳng. Ý b: Khảo sát và vẽ đồ thị hàm số \(\left( H \right)\). Ý c: Sử dụng công thức hàm giá trị tuyệt đối để rút ra cách vẽ: \(y = \left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}f\left( x \right){\rm{ khi f}}\left( x \right) \ge 0\\ - f\left( x \right){\rm{ khi f}}\left( x \right) < 0\end{array} \right.\) Lời giải chi tiết a) Tiệm cận ngang của đồ thị hàm số là đường thẳng \(y = m + 1\). Để đường thẳng này đi qua \(\left( {1;2} \right)\) thì \(2 = m + 1 \Leftrightarrow m = 1\). b) Xét đồ thị hàm số \(\left( H \right):{\rm{ }}y = \frac{{2x - 1}}{{x - 1}}\). Tập xác định: \(\mathbb{R}\backslash \left\{ 1 \right\}\). Ta có \(y' = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\forall x \ne 1\). Suy ra hàm số nghịch biến trên từng khoảng của tập xác định. Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{2x - 1}}{{x - 1}} = 2\) suy ra \(y = 2\) là tiệm cận ngang. \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 1}}{{x - 1}} = + \infty \) và \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{2x - 1}}{{x - 1}} = - \infty \) suy ra \(x = 1\) là tiệm cận đứng. Ta lập bảng biến thiên
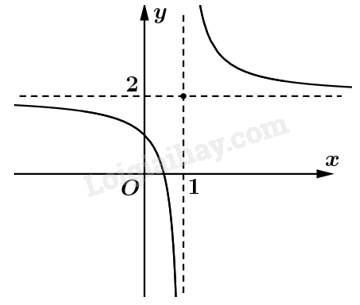
Đồ thị:
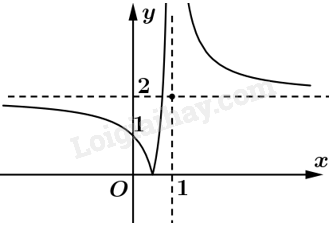
c) Ta có \(y = \left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}f\left( x \right){\rm{ khi f}}\left( x \right) \ge 0\\ - f\left( x \right){\rm{ khi f}}\left( x \right) < 0\end{array} \right.\) Để vẽ đồ thị hàm giá trị tuyệt đối ta làm như sau: Giữ nguyên phần đồ thị phía trên trục hoành, lấy đối xứng phần đồ thị nằm dưới trục hoành qua trục hoành.
|