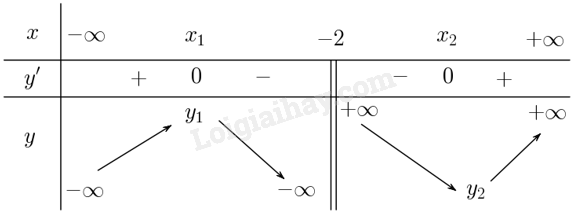
Giải bài 1.66 trang 36 sách bài tập toán 12 - Kết nối tri thứcCho hàm số (y = frac{{m{x^2} + left( {2m - 1} right)x - 1}}{{x + 2}}) với (m) là tham số. a) Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi (m > 0). b) Khảo sát và vẽ đồ thị (left( H right)) của hàm số đã cho với (m = 1). c) Giả sử (Delta ) là tiếp tuyến của đồ thị (left( H right)) tại điểm (M in left( H right)) bất kì. Chứng minh rằng nếu (Delta ) cắt tiệm cận đứng và tiệm cận xiên của (left( H right)) tại A và B thì M luôn là trung điểm của Đề bài Cho hàm số \(y = \frac{{m{x^2} + \left( {2m - 1} \right)x - 1}}{{x + 2}}\) với \(m\) là tham số. a) Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi \(m > 0\). b) Khảo sát và vẽ đồ thị \(\left( H \right)\) của hàm số đã cho với \(m = 1\). c) Giả sử \(\Delta \) là tiếp tuyến của đồ thị \(\left( H \right)\) tại điểm \(M \in \left( H \right)\) bất kì. Chứng minh rằng nếu \(\Delta \) cắt tiệm cận đứng và tiệm cận xiên của \(\left( H \right)\) tại A và B thì M luôn là trung điểm của đoạn AB. Phương pháp giải - Xem chi tiết Ý a: Xét dấu đạo hàm và lập bảng biến thiên. Ý b: Khảo sát và vẽ đồ thị hàm số \(\left( H \right)\). Ý c: Giả sử điểm M thuộc đồ thị biểu diễn tọa độ theo một tham số, từ đó viết phương trình tiếp tuyến tại M của đồ thị phụ thuộc tham số sau đó giải để tìm được tọa độ A và B theo tham số, từ đó tính toán tọa độ trung điểm sẽ suy ra điều phải chứng minh. Lời giải chi tiết a) Ta có \(y' = \frac{{\left( {2mx + 2m - 1} \right)\left( {x + 2} \right) + m{x^2} + \left( {2m - 1} \right)x - 1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{m{x^2} + 4mx + 4m - 1}}{{{{\left( {x + 2} \right)}^2}}}\). Khi đó \(y' = 0 \Leftrightarrow m{x^2} + 4mx + 4m - 1 = 0{\rm{ }}\left( {x \ne - 2} \right)\). Xét phương trình \(m{x^2} + 4mx + 4m - 1 = 0{\rm{ }}\) Ta có \(\Delta ' = {\left( {2m} \right)^2} - 4{m^2} + m = m\). Do đó nếu \(m > 0\) thì phương trình luôn có hai nghiệm phân biệt: \({x_1} = \frac{{ - 2m - \sqrt m }}{m} = - 2 - \frac{1}{{\sqrt m }}\); \({x_2} = \frac{{ - 2m + \sqrt m }}{m} = - 2 + \frac{1}{{\sqrt m }}\). Lập bảng biến thiên:
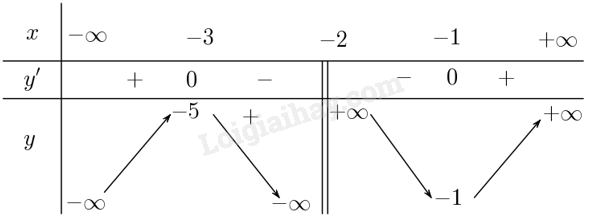
Từ bảng biến thiên suy ra hàm số luôn có tiểu và cực đại với mọi \(m > 0\). b) Với \(m = 1\) ta có \(\left( H \right):{\rm{ }}y = \frac{{{x^2} + x - 1}}{{x + 2}}\). Tập xác định: \(\mathbb{R}\backslash \left\{ { - 2} \right\}\). Ta có \(y' = \frac{{\left( {2x + 1} \right)\left( {x + 2} \right) - {x^2} - x + 1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\). Suy ra \(y' = 0 \Leftrightarrow \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}} = 0 \Leftrightarrow {x^2} + 4x + 3 = 0 \Leftrightarrow x = - 3\) hoặc \(x = - 1\). Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty \). \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{{x^2} + x - 1}}{{x + 2}} = + \infty \) và \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{{{x^2} + x - 1}}{{x + 2}} = - \infty \) suy ra \(x = - 2\) là tiệm cận đứng. Ta có \(y = \frac{{{x^2} + x - 1}}{{x + 2}} = x - 1 + \frac{1}{{x + 2}}\); \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \frac{1}{{x + 2}} = 0\) suy ra \(y = x - 1\) là tiệm cận xiên Ta lập bảng biến thiên
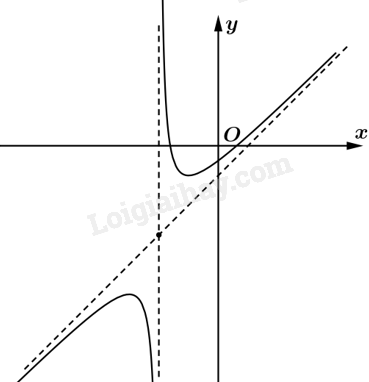
Đồ thị:
c) Giả sử \(M \in \left( H \right)\) bất kì suy ra \(M\left( {t;\frac{{{t^2} + t - 1}}{{t + 2}}} \right)\). Tiếp tuyến của \(\left( H \right)\) tại \(M\) có phương trình là \(\Delta :y = y'\left( t \right)\left( {x - t} \right) + \frac{{{t^2} + t - 1}}{{t + 2}} \Leftrightarrow y = \frac{{{t^2} + 4t + 3}}{{{{\left( {t + 2} \right)}^2}}}\left( {x - t} \right) + \frac{{{t^2} + t - 1}}{{t + 2}}\). Tiếp tuyến cắt tiệm cận đứng \(x = - 2\) tại \(A\left( { - 2; - \frac{{3t + 4}}{{t + 2}}} \right)\), cắt tiệm cận xiên \(y = x - 1\) tại \(B\left( {2t + 2;2t + 1} \right)\). Khi đó ta có \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2t = 2{x_M}\\{y_A} + {y_B} = \left( {2t + 1} \right) - \frac{{3t + 4}}{{t + 2}} = \frac{{2{t^2} + 2t - 2}}{{t + 2}} = 2{y_M}\end{array} \right.\). Vậy M là trung điểm của đoạn AB.
|