Bài 2.11 trang 48 SBT hình học 12Giải bài 2.11 trang 48 sách bài tập hình học 12. Một hình trụ có bán kính đáy bằng 50 cm và có chiều cao h = 50 cm. Đề bài Một hình trụ có bán kính đáy bằng 50 cm và có chiều cao h = 50 cm. a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên. b) Một đoạn thẳng có chiều dài 100 cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách từ đoạn thẳng đó đến trục hình trụ. Phương pháp giải - Xem chi tiết a) Diện tích xung quanh \({S_{xq}} = 2\pi Rh\). b) Xác định đoạn vuông góc chung của đoạn thẳng đó với trục hình trụ và tính toán. Lời giải chi tiết
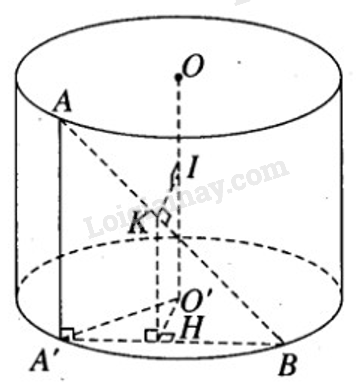
a) Ta có công thức \({S_{xq}} = 2\pi rl\) với r = 50 cm, l = 50 cm. Do đó \({S_{xq}} = 2\pi .50.50 = \pi .5000(c{m^2})\) và \(V = \pi {r^2}h = 125000.\pi (c{m^3})\) b) Giả sử đoạn thẳng AB có điểm mút A nằm trên đường tròn đáy tâm O’ . Theo giả thiết ta có: AB = 100 cm. Giả sử IK là đoạn vuông góc chung của trục OO’ và đoạn AB với I thuộc OO’ và K thuộc AB. Chiếu vuông góc đoạn AB xuống mặt phẳng đáy chứa đường tròn tâm O’ , ta có A’ , H , B lần lượt là hình chiếu của A, K, B. Vì \(KI \bot OO'\) nên IK // mp(O’BA’) , do đó O’H // IK và O’H = IK. Ta suy ra \(O'H \bot AB\) và \(O'H \bot AA'\) . Vậy \(O'H \bot A'B\) Xét tam giác vuông AA’B ta có \(A'B = \sqrt {A{B^2} - AA{'^2}} = \sqrt {{{100}^2} - {{50}^2}} = 50\sqrt 3 \) Vậy \(IK = O'H = \sqrt {O'{A^2} - A'{H^2}}\) \( = \sqrt {{{50}^2} - {{({{50\sqrt 3 } \over 2})}^2}} = 50\sqrt {1 - {3 \over 4}} = 25(cm)\) HocTot.XYZ
|