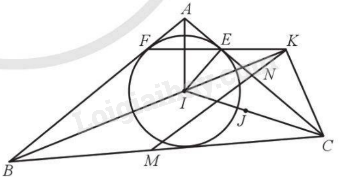
Giải bài 28 trang 92 sách bài tập toán 9 - Cánh diều tập 2Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E. Kẻ CK vuông góc với BI. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh: a) F, E, K thẳng hàng b) K, N, M thẳng hàng. Đề bài Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại F và E. Kẻ CK vuông góc với BI. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh: a) F, E, K thẳng hàng b) K, N, M thẳng hàng. Phương pháp giải - Xem chi tiết Chứng minh \(\widehat {AEF} = \widehat {KEC} = \widehat {KIC}\) suy ra F, E, K thẳng hàng. Chứng minh \(\widehat {KMC} = \widehat {NMC}\) suy ra K, N, M thẳng hàng. Lời giải chi tiết
a) Gọi J là trung điểm của IC. Do ICE và ICK là các tam giác vuông lần lượt tại E và K nên JI = JC = JE = JK do tứ giác IEKC nội tiếp đường tròn. Suy ra \(\widehat {KEC} = \widehat {KIC}\) (hai góc nội tiếp cùng chắn cung KC của đường tròn đường kính IC). Lại có \(\widehat {AEF} = {90^o} - \frac{{\widehat A}}{2}\) và \(\widehat {KIC} = \frac{{\widehat B + \widehat C}}{2} = {90^o} - \frac{{\widehat A}}{2}\). Suy ra \(\widehat {AEF} = \widehat {KEC} = \widehat {KIC}\). Vì vậy F, E, K thẳng hàng. b) Tam giác MKB cân ở M suy ra \(\widehat {KMC} = 2.\frac{{\widehat {ABC}}}{2} = \widehat {ABC}\). Lại có M, N lần lượt là trung điểm của BC, AC nên \(\widehat {NMC} = \widehat {ABC}\) (hai góc đồng vị). Suy ra \(\widehat {KMC} = \widehat {NMC}\). Vì vậy K, N, M thẳng hàng.
|