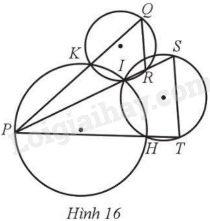
Giải bài 30 trang 93 sách bài tập toán 9 - Cánh diều tập 2Quan sát Hình 16. Chứng minh QR // ST. Đề bài Quan sát Hình 16. Chứng minh QR // ST.
Phương pháp giải - Xem chi tiết Dựa vào hình 16 chứng minh \(\widehat {QRS}\) và \(\widehat {IST}\) là hai góc so le trong nên QR // ST. Lời giải chi tiết Do các tứ giác QKIR, PKIH, IHTS đều nội tiếp đường tròn nên \(\widehat {QRS} = \widehat {QKI} = \widehat {IHP} = \widehat {IST}\). Mà \(\widehat {QRS}\) và \(\widehat {IST}\) là hai góc so le trong nên QR // ST.
|