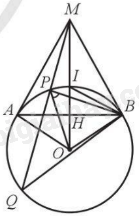
Giải bài 32 trang 93 sách bài tập toán 9 - Cánh diều tập 2Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến MA và MB với đường tròn đó (A, B là các tiếp điểm) sao cho MA = (Rsqrt 3 ) a) Xác định tâm và bán kính đường tròn nội tiếp tam giác MAB. b) Tính chu vi tam giác MAB. c) Vẽ đường thẳng d đi qua M cắt đường tròn (O) tại hai điểm P, Q. Xác định vị trí của đường thẳng d sao cho MQ + MP đạt giá trị nhỏ nhất. Đề bài Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến MA và MB với đường tròn đó (A, B là các tiếp điểm) sao cho MA = \(R\sqrt 3 \) a) Xác định tâm và bán kính đường tròn nội tiếp tam giác MAB. b) Tính chu vi tam giác MAB. c) Vẽ đường thẳng d đi qua M cắt đường tròn (O) tại hai điểm P, Q. Xác định vị trí của đường thẳng d sao cho MQ + MP đạt giá trị nhỏ nhất. Phương pháp giải - Xem chi tiết Chứng minh tam giác MAB là tam giác đều suy ra tâm và bán kính đường tròn nội tiếp tam giác MAB. Sử dụng bất đẳng thức Cosi: a2 + b2 \( \ge \) 2ab (Dấu bằng xảy ra khi và chỉ khi a = b). Lời giải chi tiết
a) Ta có MA, MB là các tiếp tuyến của đường tròn (O) lần lượt tại A và B nên MA ⊥ OA, MB ⊥ OB. Xét ∆OAM vuông tại A, theo định lí Pythagore, ta có: \(O{M^2} = M{A^2} + O{A^2} = {\left( {R\sqrt 3 } \right)^2} + {R^2} = 4{R^2}\) Suy ra OM = 2R. Gọi I là giao điểm của (O) với tia OM, ta có OI = R nên IM = OM – OI = 2R – R = R. Do đó, IM = IO = R nên I là trung điểm của OM. Do ∆OAM vuông tại A nên trung điểm I của cạnh huyền OM là tâm đường tròn ngoại tiếp ∆OAM. Do ∆OBM vuông tại B nên trung điểm I của cạnh huyền OM là tâm đường tròn ngoại tiếp ∆OBM. Do đó bốn điểm A, M, B, O cùng nằm trên đường tròn (I) đường kính OM. Vậy I là tâm đường tròn ngoại tiếp tam giác AMB. (1) Xét ∆OAM vuông tại A, ta có: \(\sin \widehat {AMO} = \frac{{OA}}{{OM}} = \frac{1}{2}\) Suy ra \(\widehat {AMO} = {30^o}\). Do MA, MB là hai tiếp tuyến của đường tròn (O) cắt nhau tại M nên MA = MB và MO là tia phân giác của góc AMB, suy ra \(\widehat {AMB} = 2\widehat {AMO} = {2.30^o} = {60^o}\) Vì vậy tam giác AMB là tam giác đều có MA = MB = AB = \(R\sqrt 3 \) (2) Từ (1), (2) suy ra đường tròn nội tiếp tam giác đều MAB cạnh \(R\sqrt 3 \)có tâm là I và bán kính là \(\frac{{R\sqrt 3 .\sqrt 3 }}{6} = \frac{R}{2}\). b) Do tam giác MAB đều cạnh \(R\sqrt 3 \) nên chu vi tam giác MAB bằng \(3R\sqrt 3 \). c) Ta có \(\widehat {MBO} = \widehat {MBP} + \widehat {PBO} = {90^o}\) suy ra \(\widehat {MBP} = {90^o} - \widehat {PBO}\) (3). Do ∆OBP cân tại O (do OB = OP) nên ta có: \(\widehat {PBO} = \widehat {BPO} = \frac{{{{180}^o} - \widehat {BOP}}}{2} = {90^o} - \frac{1}{2}\widehat {BOP}\). Xét đường tròn (O) có \(\widehat {BQP},\widehat {BOP}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BP nên \(\widehat {BQP} = \frac{1}{2}\widehat {BOP}\). Do đó \(\widehat {PBO} = {90^o} - \widehat {BQP}\) hay \(\widehat {BQP} = {90^o} - \widehat {PBO}\) (4) Từ (3) và (4) suy ra \(\widehat {MBP} = \widehat {BQP}\). Xét ∆MPB và ∆MBQ có: \(\widehat {MBP} = \widehat {MQB}\) \(\widehat {BMQ}\) là góc chung Do đó ∆MPB ᔕ ∆MBQ (g.g). Suy ra \(\frac{{MB}}{{MQ}} = \frac{{MP}}{{MB}}\) hay MP. MQ = MB2 = \({\left( {R\sqrt 3 } \right)^2} = 3{R^2}\). Lại có (MQ – MP)2 ≥ 0 hay (MQ + MP)2 ≥ 4MQ.MP Suy ra (MQ + MP)2 ≥ 4.3R2 = 12R2 Do đó \(MQ + MP \ge \sqrt {12{R^2}} = 2R\sqrt 3 \) (dấu “=” xảy ra khi MQ = MP). Vậy MQ + MP đạt giá trị nhỏ nhất bằng \(2R\sqrt 3 \), khi đó MP = MQ hay đường thẳng d đi qua M và A hoặc d đi qua M và B.
|