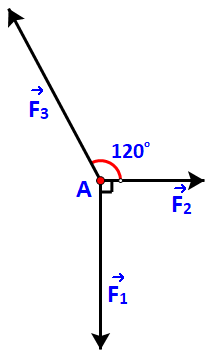
Giải bài 4.15 trang 59 SGK Toán 10 tập 1 – Kết nối tri thức

Đề bài

Chất điểm A chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) như hình 4.30 và ở trạng thái cân bằng (tức là \(\overrightarrow {{F_1}}  + \;\overrightarrow {{F_2}}  + \;\overrightarrow {{F_3}}  = \overrightarrow 0 \)). Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) biết \(\overrightarrow {{F_1}} \) có độ lớn là 20N.

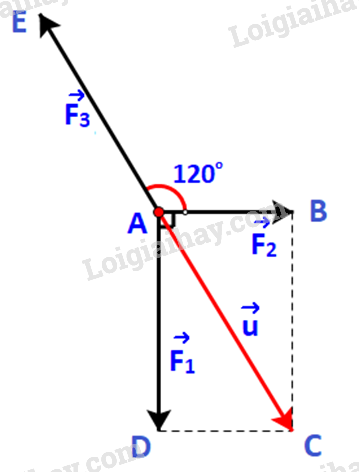
Lời giải chi tiết

Bước 1: Đặt \(\overrightarrow u  = \overrightarrow {{F_1}}  + \;\overrightarrow {{F_2}} \). Ta xác định các điểm như hình dưới.

 

Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto \(\overrightarrow u \) chính là vecto \(\overrightarrow {AC} \).

Vì chất điểm A ở trang thái cân bằng nên \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \;\overrightarrow {{F_3}}  = \overrightarrow 0 \) hay \(\overrightarrow u  + \;\overrightarrow {{F_3}}  = \overrightarrow 0 \).

\( \Leftrightarrow \overrightarrow u \) và \(\overrightarrow {{F_3}} \) là hai vecto đối nhau.

\( \Leftrightarrow A\) là trung điểm của EC.

Bước 2:

Ta có: \(\left| {\overrightarrow {{F_1}} } \right| = AD = 20,\;\left| {\overrightarrow {{F_2}} } \right| = AB,\;\left| {\overrightarrow {{F_3}} } \right| = AC\).

Do A, C, E thẳng hàng nên \(\widehat {CAB} = {180^o} - \widehat {EAB} = {60^o}\).

\(\begin{array}{l} \Rightarrow \widehat {CAD} = {90^o} - {60^o} = {30^o}\\ \Rightarrow \left\{ \begin{array}{l}AC = \frac{{AD}}{{\cos {{30}^o}}} = \frac{{40\sqrt 3 }}{3}\;\\AB = DC = AC.\sin {30^o} = \frac{{20\sqrt 3 }}{3}\end{array} \right.\end{array}\)

Vậy \(\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3}\), \(\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}\).