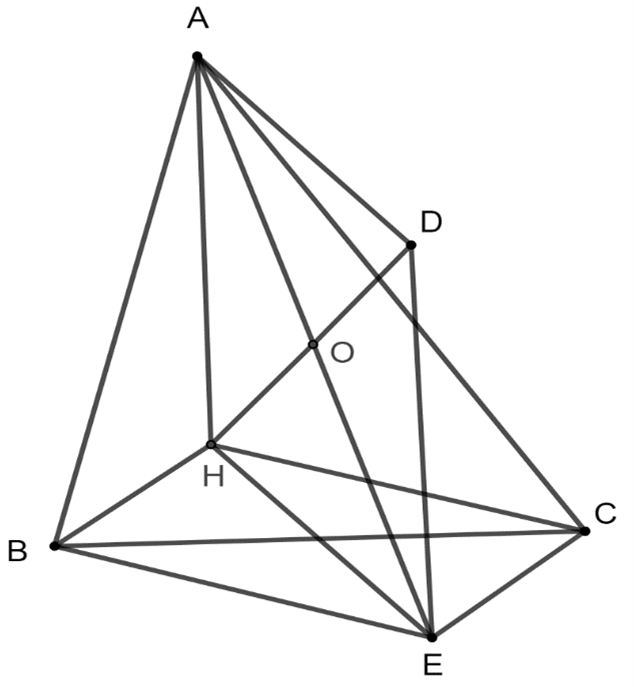
Giải bài 46 trang 92 SBT toán 10 - Cánh diềuCho tam giác nhọn ABC có các cạnh đôi một khác nhau. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác, D là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \) Đề bài Cho tam giác nhọn ABC có các cạnh đôi một khác nhau. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác, D là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \) Phương pháp giải - Xem chi tiết Bước 1: Lấy E đối xứng với A qua O Bước 2: Chứng minh các tứ giác ADEH, BHCE là hình bình hành Bước 3: Áp dụng quy tắc hình bình hành để chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \) Lời giải chi tiết
Gọi E là điểm đối xứng với A qua O . Khi đó AE là đường kính của đường tròn ngoại tiếp ∆ABC Tứ giác ADEH có O là trung điểm HD và AE nên là hình bình hành \( \Rightarrow \overrightarrow {HA} + \overrightarrow {HE} = \overrightarrow {HD} \)(1) Lại có: \(\widehat {ACE}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACE} = {90^0}\)\( \Rightarrow EC \bot AC\), mà \(BH \bot AC\) \( \Rightarrow EC//BH\) Chứng minh tương tự ta có \(BE//HC\) Tứ giác BHCE có \(EC//BH\), \(BE//HC\) nên là hình bình hành \( \Rightarrow \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HE} \)(2) Từ (1) và (2) suy ra \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HA} + \overrightarrow {HE} = \overrightarrow {HD} \) (ĐPCM)
 Chia sẻ Bình luận
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
|
