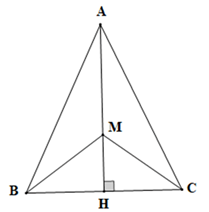
Giải Bài 53 trang 85 sách bài tập toán 7 - Cánh diềuCho tam giác ABC cân tại A có H là hình chiếu của A trên đường thẳng BC, lấy điểm M nằm giữa A và H. Chứng minh: Đề bài Cho tam giác ABC cân tại A có H là hình chiếu của A trên đường thẳng BC, lấy điểm M nằm giữa A và H. Chứng minh: a) BH = CH; b) MB = MC; c) MA < AC. Phương pháp giải - Xem chi tiết - Chứng minh: \(\Delta ABH = \Delta ACH\) suy ra BH = CH. - Chứng minh: \(\Delta ABM = \Delta ACM(c - g - c)\) suy ra BM = CM. - Chứng minh góc AMC là góc tù và sử dụng mỗi quan hệ giữa góc và cạnh đối diện để chứng minh: MA < AC Lời giải chi tiết a) Vì tam giác ABC cân tại A nên AB = AC. Xét ∆AHB và ∆AHC có: \(\widehat {AHB} = \widehat {AHC}\left( { = 90^\circ } \right)\) BA = AC (chứng minh trên), AH là cạnh chung Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông). Suy ra BH = CH (hai cạnh tương ứng). Vậy BH = CH. b) Vì ∆ABH = ∆ACH (chứng minh câu a) Suy ra \(\widehat {HAB} = \widehat {HAC}\) (hai góc tương ứng). Xét ∆AMB và ∆AMC có: BA = AC (chứng minh câu a), \(\widehat {MAB} = \widehat {MAC}\) (do \(\widehat {HAB} = \widehat {HAC}\)), AM là cạnh chung Do đó ∆ABM = ∆ACM (c.g.c). Suy ra BM = CM (hai cạnh tương ứng). Vậy BM = CM. c) Vì \(\widehat {AMC}\) là góc ngoài của tam giác CMH tại đỉnh M Nên \(\widehat {AMC} = \widehat {MHC} + \widehat {MCH}\) Mà \(\widehat {MHC} = 90^\circ \) nên \(\widehat {AMC}\) là góc tù Xét tam giác AMC có \(\widehat {AMC}\) là góc tù Nên MA < AC (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất). Vậy MA < AC.
|