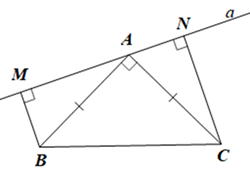
Giải Bài 56 trang 85 sách bài tập toán 7 - Cánh diềuCho tam giác ABC vuông cân tại A. Một đường thẳng a đi qua A. Gọi M và N lần lượt là hình chiếu của B và C trên đường thẳng a. Chứng minh: Đề bài Cho tam giác ABC vuông cân tại A. Một đường thẳng a đi qua A. Gọi M và N lần lượt là hình chiếu của B và C trên đường thẳng a. Chứng minh: a) \(\widehat {ABM} = \widehat {CAN}\) b) CN = MA; c) Nếu a song song với BC thì MA = AN. Phương pháp giải - Xem chi tiết - Sử dụng tổng ba góc trong một tam giác để chứng minh \(\widehat {ABM} = \widehat {CAN}\) - Chứng minh: \(\Delta MAB = \Delta NCA\) suy ra MA = NC - Chứng minh: Nếu a // BC suy ra MA = MB (1) Nếu a // BC suy ra CN = AN (2) Từ (1), (2) và câu a) suy ra MA = AN. Lời giải chi tiết a) Xét ∆MAB vuông tại M có: \(\widehat {ABM} + \widehat {MAB} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90o). Ta có \(\widehat {MAB} + \widehat {BAC} + \widehat {CAN} = 180^\circ \) Suy ra \(\widehat {MAB} + \widehat {CAN} = 180^\circ - \widehat {BAC} = 90^\circ \) Lại có \(\widehat {ABM} + \widehat {MAB} = 90^\circ \) Suy ra \(\widehat {ABM} = \widehat {CAN}\) Vậy \(\widehat {ABM} = \widehat {CAN}\) b) Xét ∆MAB và ∆NCA có: \(\widehat {BMA} = \widehat {ANC}\left( { = 90^\circ } \right)\) BA = AC (vì tam giác ABC vuông cân tại A), \(\widehat {ABM} = \widehat {CAN}\) (chứng minh câu a). Do đó ∆MAB = ∆NCA (cạnh huyền – góc nhọn). Suy ra MA = NC (hai cạnh tương ứng). Vậy MA = NC. c) Vì tam giác ABC cân tại A nên \(\widehat {ACB} = \widehat {ABC}\) Lại có \(\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = 180^\circ \) (tổng ba góc của tam giác ABC) Suy ra \(\widehat {ACB} = \widehat {ABC} = \frac{{180^\circ - 90^\circ }}{2} = 45^\circ \) • Nếu a // BC thì \(\widehat {MAB} = \widehat {ABC}\) (hai góc so le trong). Do đó \(\widehat {MAB} = 45^\circ \) Xét ∆ABM có \(\widehat {AMB} + \widehat {MBA} + \widehat {MAB} = 180^\circ \) (tổng ba góc của một tam giác) Suy ra \(\widehat {MBA} = 180^\circ - \widehat {AMB} - \widehat {MAB} = 180^\circ - 90^\circ - 45^\circ = 45^\circ \) Do đó \(\widehat {MAB} = \widehat {MBA}\) (cùng bằng 45°). Xét ∆AMB có \(\widehat {AMB} = 90^\circ \) và \(\widehat {MAB} = \widehat {MBA}\) nên ∆AMB vuông cân tại M. Suy ra MA = MB (1) • Nếu a // BC thì \(\widehat {CAN} = \widehat {ACB} = 45^\circ \) (hai góc so le trong) Xét ∆ABM có \(\widehat {ACN} + \widehat {ANC} + \widehat {CAN} = 180^\circ \) (tổng ba góc của một tam giác) Suy ra \(\widehat {ACN} = 180^\circ - \widehat {ANC} - \widehat {CAN} = 180^\circ - 90^\circ - 45^\circ = 45^\circ \) Do đó \(\widehat {ACN} = \widehat {CAN}\) (cùng bằng 45°). Xét ∆ANC có \(\widehat {ANC} = 90^\circ \) và \(\widehat {ACN} = \widehat {CAN}\) nên ∆ANC vuông cân tại N. Suy ra CN = AN (2) Từ (1) và (2) suy ra MA = AN. Vậy MA = AN.
|