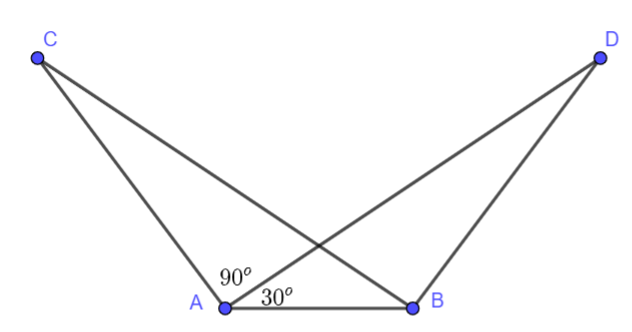
Giải bài 6 trang 66 vở thực hành Toán 7

Đề bài

Bài 6. Cho hình vẽ dưới đây, biết rằng AC = BD, BC = AD, $\widehat {CAD} = {90^o},\widehat {DAB} = {30^o}$. Chứng minh rằng $\Delta ABC = \Delta BAD$

Lời giải chi tiết

Theo hình vẽ ta có

$\widehat {CAB} = \widehat {CAD} + \widehat {DAB} = {90^o} + {30^o} = {120^o}$

Hai tam giác ABC và BAD có:

AC = BD, BC = AD, AB là cạnh chung

Vậy $\Delta ABC = \Delta BAD$ (c.c.c).

Từ đây suy ra $\widehat {ABC} = \widehat {DAB} = {30^o},\widehat {ABD} = \widehat {CAB} = {120^o}$

Do tổng ba góc trong tam giác ABC bằng ${180^o}$ nên ta có

$\widehat {ACB} = {180^o} - \widehat {CAB} + \widehat {ABC} = {180^o} - {120^o} - {30^o} = {30^o}$

Vì $\Delta ABC = \Delta BAD$ nên $\widehat {BDA} = \widehat {ACB} = {30^o}$. Hai tam giác ABC và BDA có:

$\widehat {ABC} = \widehat {DAB} = {30^o}$

BC = AD ( theo giả thiết)

$\widehat {BDA} = \widehat {ACB} = {30^o}$

Vậy $\Delta ABC = \Delta BAD$ (g.c.g)