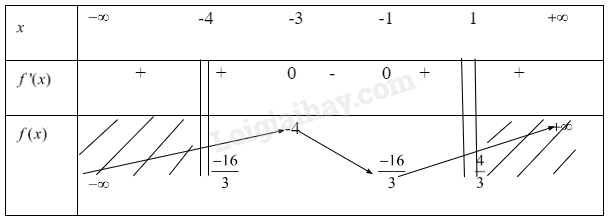
Giải bài tập 1.10 trang 14 SGK Toán 12 tập 1 - Cùng khám pháTìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\) b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\) c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\)trên nửa khoảng \([2;6)\) d) \(y = f(x) = \sqrt {4 - {x^2}} \) e) \(y = f(x) = {e^x} - x\)trên đoạn \([ - 1;2]\) f) \(y = f(x) = x\ln x\)trên đoạn \([{e^{ - 2}};e]\) Đề bài Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\) b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\) c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) trên nửa khoảng \([2;6)\) d) \(y = f(x) = \sqrt {4 - {x^2}} \) e) \(y = f(x) = {e^x} - x\) trên đoạn \([ - 1;2]\) f) \(y = f(x) = x\ln x\) trên đoạn \([{e^{ - 2}};e]\) Phương pháp giải - Xem chi tiết Bước 1 Tính \(f'(x)\) Bước 2 Lập bảng biến thiên Bước 3 Tìm cực trị của hàm số trên đoạn Bước 4 Suy ra điểm có giá trị lớn nhất, điểm có giá trị bé nhất của hàm số trên các khoảng Lời giải chi tiết a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\) Hàm số trên xác định trên R Ta có \(f'(x) = {x^2} + 4x + 3\) Xét \(f'(x) = 0\) \( \Rightarrow {x^2} + 4x + 3 = 0\) \( \Rightarrow \left[ \begin{array}{l}x = - 1\\x = - 3\end{array} \right.\) Ta có bảng biến thiên
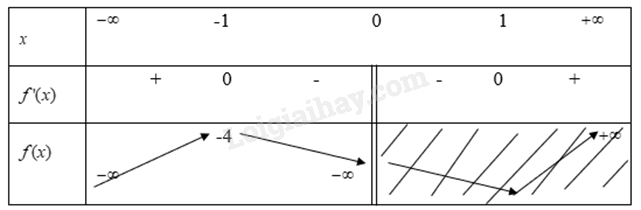
Từ bảng biến thiên ta có Hàm số \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) đạt GTLN trên đoạn \([ - 4;1]\) tại x = 1 khi đó y = \(\frac{4}{3}\) Hàm số \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) đạt GTNN trên đoạn \([ - 4;1]\) tại x = -4 và x= -1 khi đó y = \(\frac{{ - 16}}{3}\) b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\) Hàm số trên xác định trên R/{0} Ta có \(f'(x) = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\) Xét \(f'(x) = 0\) \( \Rightarrow {x^2} - 1 = 0\) \( \Rightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\) Ta có bảng biến thiên
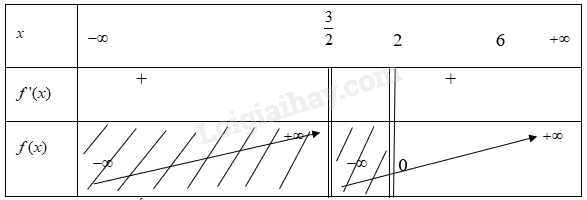
Vậy hàm số \(y = f(x) = x + \frac{1}{x} - 2\) đạt GTLN trên khoảng \(( - \infty ;0)\) tại x=-1 khi đó y=-4 c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) trên nửa khoảng \([2;6)\) Hàm số xác định trên R/\(\left\{ {\frac{3}{2}} \right\}\) Ta có \(f'(x) = \frac{1}{{{{(2x - 3)}^2}}}\) Vì \(f'(x) > 0\) với \(x \in R/\left\{ {\frac{3}{2}} \right\}\) Nên hàm số luôn đồng biến với \(x \in R/\left\{ {\frac{3}{2}} \right\}\) Khi đó ta có bảng biến thiên
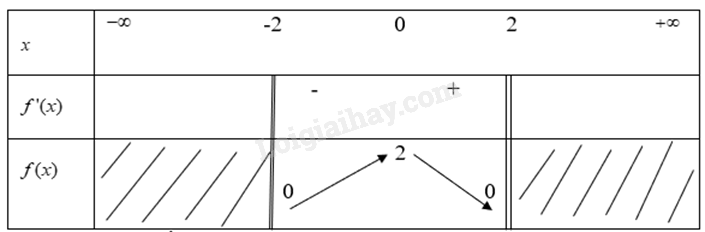
Từ bảng biến thiên ta có: Hàm số \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) đạt GTNN trên nửa khoảng \([2;6)\) tại x = 2 khi đó y = 0 d) \(y = f(x) = \sqrt {4 - {x^2}} \) Hàm số xác định với \(\begin{array}{l}x \in [ - 2;2]\\\end{array}\) Ta có \(f'(x) = \frac{{ - 2x}}{{2\sqrt {4 - {x^2}} }}\) Xét \(f'(x) = 0\)\( \Rightarrow x = 0\) Từ đó ta có bảng biến thiên
Từ bảng biến thiên, ta có: Hàm sô \(y = f(x) = \sqrt {4 - {x^2}} \) đạt GTLN tại x = 0 khi đó y =2 Hàm sô \(y = f(x) = \sqrt {4 - {x^2}} \) đạt GTNN tại x = 2 và x= -2 khi đó y =2 e) \(y = f(x) = {e^x} - x\) trên khoảng \([ - 1;2]\) Hàm số xác định trên R Ta có \(f'(x) = {e^x} - 1\) Xét \(f'(x) = 0\) \( \Rightarrow {e^x} - 1 = 0\) \( \Rightarrow x = 0\) Từ đó ta có bảng biến thiên
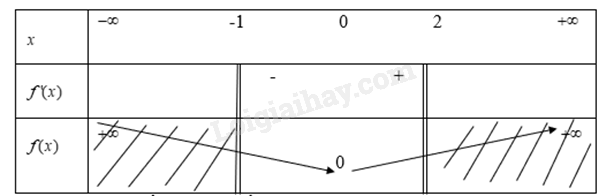
Từ bảng biến thiên ta thấy Hàm số\(y = f(x) = {e^x} - x\) đạt GTNN trên khoảng\([ - 1;2]\) tại x=0 khi đó y=0 Hàm số\(y = f(x) = {e^x} - x\) đạt GTNN trên khoảng\([ - 1;2]\) tại x=2 khi đó y=5,9 f) \(y = f(x) = x\ln x\) trên khoảng \([{e^{ - 2}};e]\) Hàm số trên xác định với \(x \in \left( {0; + \infty } \right)\) Ta có \(f'(x) = \ln x + 1\) Xét \(f'(x) = \ln x + 1\) \( \Rightarrow x = {e^{ - 1}}\) Từ đó ta có bảng biến thiên là
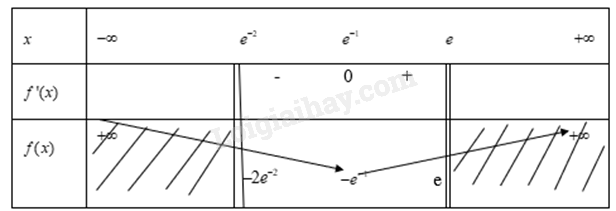
Từ bảng biến thiên ta có: Hàm số\(y = f(x) = x\ln x\) đạt GTLN trên khoảng \([{e^{ - 2}};e]\) tại x=e khi đó y=e Hàm số\(y = f(x) = x\ln x\) đạt GTLN trên khoảng \([{e^{ - 2}};e]\) tại x= \({e^{ - 1}}\) khi đó y= \( - {e^{ - 1}}\)
|