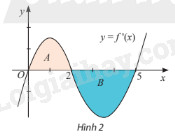
Giải bài tập 12 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạoCho hàm số (y = fleft( x right)). Đồ thị của hàm số (y = f'left( x right)) là đường cong trong hình dưới đây. Biết rằng diện tích các phần hình phẳng (A) và (B) lần lượt là ({S_A} = 2) và ({S_B} = 3). Nếu (fleft( 0 right) = 4) thì giá trị của (fleft( 5 right)) bằng A. (3) B. (5) C. (9) D. ( - 1) Đề bài Cho hàm số \(y = f\left( x \right)\). Đồ thị của hàm số \(y = f'\left( x \right)\) là đường cong trong hình 2. Biết rằng diện tích các phần hình phẳng \(A\) và \(B\) lần lượt là \({S_A} = 2\) và \({S_B} = 3\). Nếu \(f\left( 0 \right) = 4\) thì giá trị của \(f\left( 5 \right)\) bằng
A. \(3\) B. \(5\) C. \(9\) D. \( - 1\) Phương pháp giải - Xem chi tiết Sử dụng công thức tính diện tích hình phẳng của hình \(A\) để tính \(f\left( 2 \right)\). Sử dụng công thức tính diện tích hình phẳng của hình \(B\) để tính \(f\left( 5 \right)\). Lời giải chi tiết Hình phẳng \(A\) được giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), trục hoành (\(y = 0\)), trục tung (\(x = 0\)) và đường thẳng \(x = 2\) nên diện tích hình phẳng \(A\) là \({S_A} = \int\limits_0^2 {\left| {f'\left( x \right)} \right|dx} = \int\limits_0^2 {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_0^2 = f\left( 2 \right) - f\left( 0 \right)\) Suy ra \(f\left( 2 \right) = {S_A} + f\left( 0 \right) = 2 + 4 = 6\) Hình phẳng \(B\) được giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), trục hoành và các đường thẳng \(x = 2\), \(x = 5\) nên diện tích hình phẳng \(B\) là \({S_B} = \int\limits_2^5 {\left| {f'\left( x \right)} \right|dx} = - \int\limits_2^5 {f'\left( x \right)dx} = \left. { - f\left( x \right)} \right|_2^5 = - f\left( 5 \right) + f\left( 2 \right)\) Do đó \(f\left( 5 \right) = - \left( {{S_B} - f\left( 2 \right)} \right) = - \left( {3 - 6} \right) = 3\) Đáp án đúng là A.
|