Giải bài tập 2 trang 41 SGK Toán 12 tập 1 - Cánh diềuđường cong ở hình 29 là đồ thị của hàm số : Đề bài
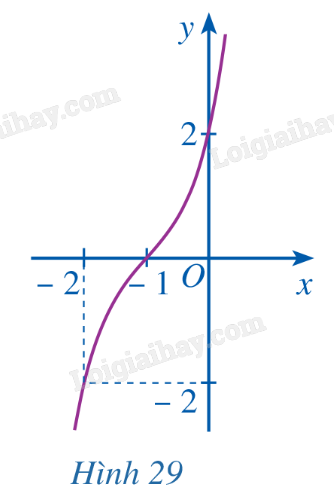
Đường cong ở hình 29 là đồ thị của hàm số:
A. $y = x^3 + x^2 + 2x + 2$. B. $y = -x^3 - 4x^2 - x + 2$. C. $y = x^3 + 3x^2 - 4x + 2$. D. $y = x^3 + 3x^2 + 4x + 2$. Phương pháp giải - Xem chi tiết + Xét đồng biến nghịch biến của hàm số. + Tìm giao điểm trục tung và trục hoành. + Xét hàm số. Lời giải chi tiết Hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\). Đồ thị hàm số giao với trục tung tại điểm (0;2) giao với trục hoành tại (-1;0). Chọn D
|