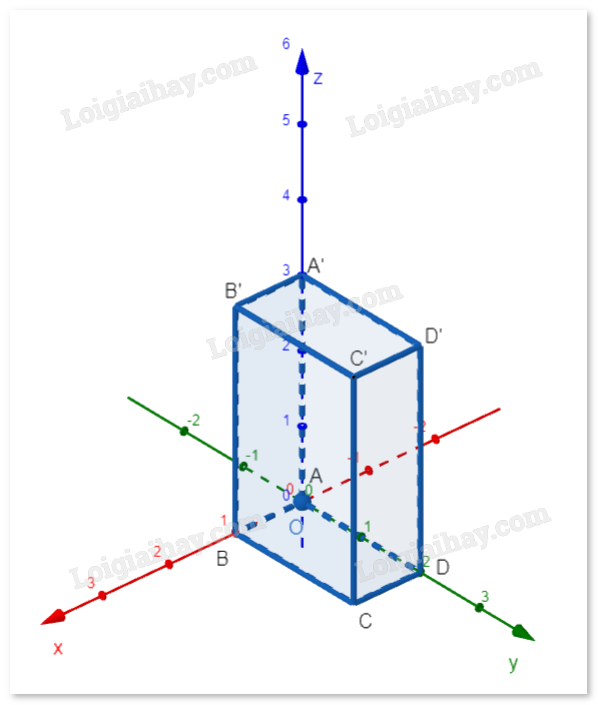
Giải bài tập 2.25 trang 82 SGK Toán 12 tập 1 - Cùng khám pháTrong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc tọa độ O, các đỉnh B, D, A’ tương ứng thuộc các tia Ox, Oy, Oz và AB = 1, AD = 2, AA’ = 3. a) Tìm tọa độ các đỉnh của hình hộp. b) Tìm điểm E trên đường thẳng DD’ sao cho \(B'E \bot A'C'\). Đề bài Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc tọa độ O, các đỉnh B, D, A’ tương ứng thuộc các tia Ox, Oy, Oz và AB = 1, AD = 2, AA’ = 3. a) Tìm tọa độ các đỉnh của hình hộp. b) Tìm điểm E trên đường thẳng DD’ sao cho \(B'E \bot A'C'\). Phương pháp giải - Xem chi tiết a) Sử dụng thông tin về các cạnh của hình hộp để xác định tọa độ của các đỉnh. b) Tìm vectơ chỉ phương của đường thẳng DD’ và B’E. Sử dụng điều kiện \(B'E \bot A'C'\) để thiết lập phương trình và giải tìm tọa độ của E. Lời giải chi tiết
a) Tọa độ các đỉnh của hình hộp chữ nhật là: - A trùng với gốc tọa độ, tức A(0; 0; 0) . - B thuộc tia Ox , nên B(1; 0; 0) (vì AB = 1 ). - D thuộc tia Oy , nên D(0; 2; 0) (vì AD = 2 ). - A’ thuộc tia Oz , nên A’(0; 0; 3) (vì AA’ = 3 ). Các đỉnh còn lại của hình hộp chữ nhật: - C đối với A qua BD , tọa độ là C(1; 2; 0) . - B’ đối với A qua A’C , tọa độ là B’(1; 0; 3) . - D’ đối với A qua A’D , tọa độ là D’(0; 2; 3) . - C’ đối với A qua B’D , tọa độ là C’(1; 2; 3) . b) Tọa độ của điểm E trên đường thẳng DD’ : - Đường thẳng DD’ có phương trình dạng: \(x = 0,\quad y = 2,\quad z = t{\rm{.}}\) với t là tham số. Tọa độ của E là E(0; 2; t) . Để \(B'E \bot A'C\), cần: \(\overrightarrow {B'E} \cdot \overrightarrow {A'C} = 0\) Tính các vectơ: \(\overrightarrow {B'E} = (0 - 1;2 - 0;t - 3) = ( - 1;2;t - 3)\) \(\overrightarrow {A'C} = (1 - 0;2 - 0;0 - 3) = (1;2; - 3)\) Điều kiện vuông góc: \(\overrightarrow {BE} \cdot \overrightarrow {A'C} = ( - 1) \times 1 + 2 \times 2 + (t - 3) \times ( - 3) = - 1 + 4 - 3t + 9 = 0\) Giải phương trình này: \( - 1 + 4 - 3t + 9 = 0\quad \Rightarrow \quad 12 = 3t\quad \Rightarrow \quad t = 4\) Vậy tọa độ của E là E(0; 2; 4) .
|