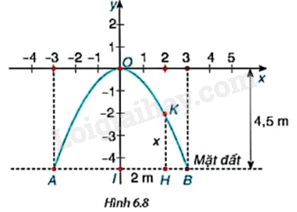
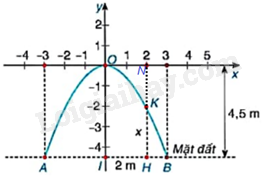
Giải bài tập 6.7 trang 9 SGK Toán 9 tập 2 - Kết nối tri thức

Đề bài

Một cổng vòm được thiết kế dạng parabol $y = a{x^2}$ như Hình 6.8. Biết chiều rộng của chân cổng là $AB = 6m$ và chiều cao của cổng là $OI = 4,5m$.

a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2m.

b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2m, chiều cao 3m. Hỏi xe tải này có thể đi qua được cổng vòm hay không?

Lời giải chi tiết

a)

Đồ thị hàm số $y = a{x^2}$ đi qua điểm $\left( {3; - \frac{9}{2}} \right)$ nên ta có:

$- \frac{9}{2} = a{.3^2} \Rightarrow a =  - \frac{1}{2}$.

Khi đó, $y =  - \frac{1}{2}{x^2}$.

Ta có: $H(2;-4,5)$; $K(2;y_K)$

Vì K thuộc đồ thị hàm số $y =  - \frac{1}{2}{x^2}$ nên $y_K = -\frac{1}{2}{2^2}= -2$ nên $K(2;-2)$

Từ đó ta có: $HK = 4,5 - 2 = 2,5\left( m \right)$.

b) Cổng vòm có chiều cao bằng $OI = 4,5m$ và chiều rộng $AB = 6m$.

Với $x = 1$ thì $y =  - \frac{1}{2}{.1^2} =  - \frac{1}{2}$.

Vì $4,5 - \left| { - \frac{1}{2}} \right| > 3$ nên xe tải này có thể đi qua cổng vòm được.