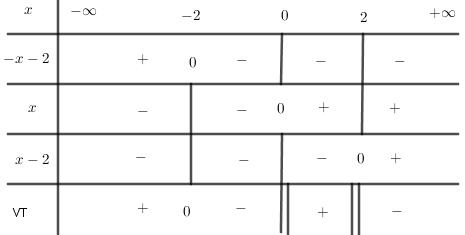
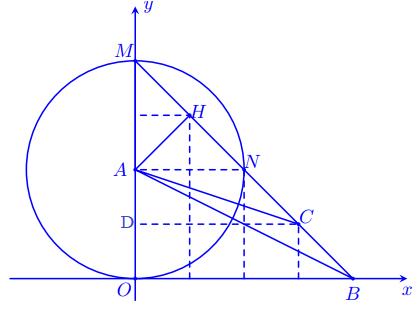
Giải đề thi học kì 2 toán lớp 10 năm 2019 - 2020 Sở GD&ĐT Bắc NinhGiải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 Sở GD&ĐT Bắc Ninh với cách giải nhanh và chú ý quan trọng Đề bài Câu 1 (3,5 điểm): Giải phương trình và bất phương trình: a) \(\sqrt {2x - 7} = 1\) b) \(\left| {x - 1} \right| = 3\) c) \(2{x^2} - x \le x\left( {x + 4} \right) + 6\) d) \(\dfrac{1}{x} > \dfrac{2}{{x - 2}}\) Câu 2 (2,0 điểm): Cho \(\sin \alpha = \dfrac{4}{5}\) với \(0 < \alpha < \dfrac{\pi }{2}\). a) Tính \(\cos \alpha \) và \(\tan \alpha \). b) Tính \(\sin \dfrac{{5\alpha }}{2}\). Câu 3 (3,5 điểm): Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {0;2} \right),B\left( {4;0} \right)\) và trọng tâm \(G\left( {\dfrac{7}{3};1} \right)\). a) Tìm tọa độ đỉnh \(C\). Viết phương trình tổng quát của đường thẳng \(BC\). b) Viết phương trình đường tròn \(\left( T \right)\) tâm \(A\) và cắt đường thẳng \(BC\) tại hai điểm phân biệt \(M,N\) thỏa mãn \(MN = 2\sqrt 2 \). c) Tính diện tích tứ giác \(AOBC\). Câu 4 (1,0 điểm): Cho \(a,b,c\) là độ dài ba cạnh của một tam giác có chu vi bằng \(2\). Chứng minh rằng \(21\left( {{a^2} + {b^2} + {c^2}} \right) \ge 20 + 9\left( {{a^3} + {b^3} + {c^3}} \right)\) Lời giải chi tiết HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn HocTot.XYZ Câu 1 (VD): Phương pháp: a) Bình phương hai vế. b) Sử dụng \(\left| {f\left( x \right)} \right| = a > 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\\f\left( x \right) = - a\end{array} \right.\) c) Rút gọn bất phương trình về bất phương trình bậc hai và giải bất phương trình có được. d) Chuyển vế, biến đổi về tích, thương các nhị thức bậc nhất. Xét dấu và suy ra tập nghiệm. Cách giải: Giải phương trình và bất phương trình: a) \(\sqrt {2x - 7} = 1\) ĐK: \(2x - 7 \ge 0 \Leftrightarrow 2x \ge 7\) \( \Leftrightarrow x \ge \dfrac{7}{2}\) \(\begin{array}{l}\sqrt {2x - 7} = 1\\ \Leftrightarrow 2x - 7 = 1\\ \Leftrightarrow 2x = 8\\ \Leftrightarrow x = 4\left( {TM} \right)\end{array}\) Vậy \(S = \left\{ 4 \right\}\). b) \(\left| {x - 1} \right| = 3\) \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}x - 1 = 3\\x - 1 = - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 2\end{array} \right.\end{array}\) Vậy \(S = \left\{ {4; - 2} \right\}\). c) \(2{x^2} - x \le x\left( {x + 4} \right) + 6\) \(\begin{array}{l} \Leftrightarrow 2{x^2} - x \le {x^2} + 4x + 6\\ \Leftrightarrow {x^2} - 5x - 6 \le 0\\ \Leftrightarrow - 1 \le x \le 6\end{array}\) Vậy \(S = \left[ { - 1;6} \right]\). d) \(\dfrac{1}{x} > \dfrac{2}{{x - 2}}\) ĐK: \(\left\{ \begin{array}{l}x \ne 0\\x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 2\end{array} \right.\). \(\begin{array}{l}\dfrac{1}{x} > \dfrac{2}{{x - 2}}\\ \Leftrightarrow \dfrac{1}{x} - \dfrac{2}{{x - 2}} > 0\\ \Leftrightarrow \dfrac{{x - 2 - 2x}}{{x\left( {x - 2} \right)}} > 0\\ \Leftrightarrow \dfrac{{ - x - 2}}{{x\left( {x - 2} \right)}} > 0\end{array}\) Ta có: \( - x - 2 = 0 \Leftrightarrow x = - 2\) Lập bảng xét dấu ta được: Từ bảng xét dấu ta thấy \(VT > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 2\\0 < x < 2\end{array} \right.\) Vậy \(S = \left( { - \infty ; - 2} \right) \cup \left( {0;2} \right)\). Câu 2 (VD): Phương pháp: a) Sử dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), kết hợp điều kiện của \(\alpha \) tìm \(\cos \alpha \). Sử dụng công thức \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\) tính \(\tan \alpha \). b) Tính lần lượt các giá trị \(\sin 2\alpha ,\cos 2\alpha ,\sin \dfrac{\alpha }{2},\cos \dfrac{\alpha }{2}\). Thay vào công thức \(\sin \dfrac{{5\alpha }}{2} = \sin \left( {2\alpha + \dfrac{\alpha }{2}} \right)\) để tính toán. Cách giải: Cho \(\sin \alpha = \dfrac{4}{5}\) với \(0 < \alpha < \dfrac{\pi }{2}\). a) Tính \(\cos \alpha \) và \(\tan \alpha \). Ta có: \(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\ \Rightarrow {\left( {\dfrac{4}{5}} \right)^2} + {\cos ^2}\alpha = 1\\ \Rightarrow {\cos ^2}\alpha = 1 - \dfrac{{16}}{{25}} = \dfrac{9}{{25}}\end{array}\) Vì \(0 < \alpha < \dfrac{\pi }{2}\) nên \(\alpha \) thuộc góc phần tư thứ nhất, do đó \(\cos \alpha > 0\). \( \Rightarrow \cos \alpha = \sqrt {\dfrac{9}{{16}}} = \dfrac{3}{5}\). \( \Rightarrow \tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }} = \dfrac{4}{5}:\dfrac{3}{5} = \dfrac{4}{3}\). Vậy \(\cos \alpha = \dfrac{3}{5};\tan \alpha = \dfrac{4}{3}\). b) Tính \(\sin \dfrac{{5\alpha }}{2}\). Ta có: \(\sin 2\alpha = 2\sin \alpha \cos \alpha \) \( = 2.\dfrac{4}{5}.\dfrac{3}{5} = \dfrac{{24}}{{25}}\) \(\cos 2\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \) \( = {\left( {\dfrac{3}{5}} \right)^2} - {\left( {\dfrac{4}{5}} \right)^2} = - \dfrac{7}{{25}}\) \({\sin ^2}\dfrac{\alpha }{2} = \dfrac{{1 - \cos \alpha }}{2} = \dfrac{{1 - \dfrac{3}{5}}}{2} = \dfrac{1}{5}\) Mà \(0 < \alpha < \dfrac{\pi }{2} \Rightarrow 0 < \dfrac{\alpha }{2} < \dfrac{\pi }{4}\) \( \Rightarrow \sin \dfrac{\alpha }{2} > 0\) Do đó \(\sin \dfrac{\alpha }{2} = \sqrt {\dfrac{1}{5}} = \dfrac{1}{{\sqrt 5 }}\). \({\cos ^2}\dfrac{\alpha }{2} = \dfrac{{1 + \cos \alpha }}{2} = \dfrac{{1 + \dfrac{3}{5}}}{2} = \dfrac{4}{5}\) Mà \(0 < \alpha < \dfrac{\pi }{2} \Rightarrow 0 < \dfrac{\alpha }{2} < \dfrac{\pi }{4}\) \( \Rightarrow \cos \dfrac{\alpha }{2} > 0\) Do đó \(\cos \dfrac{\alpha }{2} = \sqrt {\dfrac{4}{5}} = \dfrac{2}{{\sqrt 5 }}\). \(\begin{array}{l} \Rightarrow \sin \dfrac{{5\alpha }}{2} = \sin \left( {2\alpha + \dfrac{\alpha }{2}} \right)\\ = \sin 2\alpha \cos \dfrac{\alpha }{2} + \cos 2\alpha \sin \dfrac{\alpha }{2}\\ = \dfrac{{24}}{{25}}.\dfrac{2}{{\sqrt 5 }} + \left( { - \dfrac{7}{{25}}} \right).\dfrac{1}{{\sqrt 5 }}\\ = \dfrac{{41}}{{25\sqrt 5 }} = \dfrac{{41\sqrt 5 }}{{125}}\end{array}\) Vậy \(\sin \dfrac{{5\alpha }}{2} = \dfrac{{41\sqrt 5 }}{{125}}\). Câu 3 (VD ): Phương pháp: a) Sử dụng công thức trọng tâm \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\) để tìm tọa độ \(C\). Đường thẳng \(BC\) đi qua điểm \(B\) và nhận \(\overrightarrow {BC} \) làm VTCP. b) Gọi \(H\) là trung điểm của \(MN\). Khi đó \(R = \sqrt {A{H^2} + H{M^2}} \). Từ đó viết được phương trình đường tròn tâm \(A\) bán kính \(R\) theo công thức \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\). c) Lần lượt tính diện tích các tam giác \(ABC\) và \(AOB\) rồi cộng các kết quả lại với nhau. Cách giải: Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {0;2} \right),B\left( {4;0} \right)\) và trọng tâm \(G\left( {\dfrac{7}{3};1} \right)\). a) Tìm tọa độ đỉnh \(C\). Viết phương trình tổng quát của đường thẳng \(BC\). Ta có: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\) \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\dfrac{7}{3} = \dfrac{{0 + 4 + {x_C}}}{3}\\1 = \dfrac{{2 + 0 + {y_C}}}{3}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}7 = 4 + {x_C}\\3 = 2 + {y_C}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3\\{y_C} = 1\end{array} \right.\\ \Rightarrow C\left( {3;1} \right)\end{array}\) Ta có: \(\overrightarrow {BC} = \left( { - 1;1} \right)\). Đường thẳng \(BC\) nhận \(\overrightarrow {BC} = \left( { - 1;1} \right)\) làm VTCP nên nhận \(\overrightarrow n = \left( {1;1} \right)\) làm VTPT. \(BC\) đi qua \(B\left( {4;0} \right)\) nên có phương trình: \(1\left( {x - 4} \right) + 1\left( {y - 0} \right) = 0\) \( \Leftrightarrow x + y - 4 = 0\). Vậy \(C\left( {3;1} \right)\) và \(BC:x + y - 4 = 0\). b) Viết phương trình đường tròn \(\left( T \right)\) tâm \(A\) và cắt đường thẳng \(BC\) tại hai điểm phân biệt \(M,N\) thỏa mãn \(MN = 2\sqrt 2 \). Gọi \(H\) là trung điểm của \(MN\) thì \(HM = HN = \dfrac{{MN}}{2} = \sqrt 2 \). Ta có: \(AH = d\left( {A,BC} \right)\) \( = \dfrac{{\left| {0 + 2 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{2}{{\sqrt 2 }} = \sqrt 2 \) Tam giác \(AHM\) vuông tại \(H\) nên theo Pitago ta có: \(R = AM = \sqrt {A{H^2} + H{M^2}} \) \( = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} = 2\) Vậy phương trình đường tròn \(\left( T \right)\) là: \({\left( {x - 0} \right)^2} + {\left( {y - 2} \right)^2} = {2^2}\) hay \({x^2} + {\left( {y - 2} \right)^2} = 4\). c) Tính diện tích tứ giác \(AOBC\). Ta có: \(BC = \sqrt {{{\left( {3 - 4} \right)}^2} + {{\left( {1 - 0} \right)}^2}} = \sqrt 2 \) \( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AH.BC\) \( = \dfrac{1}{2}.\sqrt 2 .\sqrt 2 = 1\) (đvdt) \({S_{AOB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.4.2 = 4\) (đvdt) Vậy \({S_{AOBC}} = {S_{ABC}} + {S_{AOB}}\) \( = 1 + 4 = 5\) (đvdt). Cách khác: \({S_{ADC}} = \dfrac{1}{2}AD.DC\) \( = \dfrac{1}{2}.1.3 = \dfrac{3}{2}\) (đvdt) \({S_{DCBO}} = \dfrac{1}{2}\left( {DC + OB} \right).DO\) \( = \dfrac{1}{2}.\left( {3 + 4} \right).1 = \dfrac{7}{2}\) (đvdt) Vậy \({S_{AOBC}} = {S_{ADC}} + {S_{DCBO}}\) \( = \dfrac{3}{2} + \dfrac{7}{2} = 5\) (đvdt). Câu 4 (VDC): Phương pháp: - Sử dụng bất đẳng thức tam giác nhận xét \(a,b,c\). - Xuất phát từ bất đẳng thức \(\left( {1 - a} \right){\left( {a - \dfrac{2}{3}} \right)^2} \ge 0\) rút ra \(21{a^2} \ge 9{a^3} + 16a - 4\). Tương tự với \(b,c\), từ đó suy ra đpcm. Cách giải: Cho \(a,b,c\) là độ dài ba cạnh của một tam giác có chu vi bằng \(2\). Chứng minh rằng \(21\left( {{a^2} + {b^2} + {c^2}} \right) \ge 20 + 9\left( {{a^3} + {b^3} + {c^3}} \right)\) Tam giác có chu vi bằng \(2\) nên \(a + b + c = 2\). \(a,b,c\) là ba cạnh của tam giác nên \(a < b + c\) \( \Rightarrow 2a < a + b + c = 2 \Rightarrow a < 1\). Tương tự ta cũng có \(b,c < 1\) nên \(a,b,c \in \left( {0;1} \right)\). Ta có: \(\begin{array}{l}21\left( {{a^2} + {b^2} + {c^2}} \right) \ge 20 + 9\left( {{a^3} + {b^3} + {c^3}} \right)\\ \Leftrightarrow 9\left( {{a^3} + {b^3} + {c^3}} \right) - 21\left( {{a^2} + {b^2} + {c^2}} \right) \\+ 20 \le 0\\ \Leftrightarrow 9\left( {{a^3} + {b^3} + {c^3}} \right) - 21\left( {{a^2} + {b^2} + {c^2}} \right)\\ + 16\left( {a + b + c} \right) - 12 \le 0\\ \Leftrightarrow 9{a^3} + 9{b^3} + 9{c^3} - 21{a^2} - 21{b^2} - 21{c^2}\\ + 16a + 16b + 16c - 4 - 4 - 4 \le 0\\ \Leftrightarrow \left( {9{a^3} - 21{a^2} + 16a - 4} \right)\\ + \left( {9{b^3} - 21{b^2} + 16b - 4} \right)\\ + \left( {9{c^3} - 21{c^2} + 16c - 4} \right) \le 0\\ \Leftrightarrow \left( {a - 1} \right)\left( {9{a^2} - 12a + 4} \right)\\ + \left( {b - 1} \right)\left( {9{b^2} - 12b + 4} \right)\\ + \left( {c - 1} \right)\left( {9{c^2} - 12c + 4} \right) \le 0\\ \Leftrightarrow \left( {a - 1} \right){\left( {3a - 2} \right)^2}\\ + \left( {b - 1} \right){\left( {3b - 2} \right)^2}\\ + \left( {c - 1} \right){\left( {3c - 2} \right)^2} \le 0\end{array}\) Dễ thấy \(a < 1 \Rightarrow a - 1 < 0\) và \({\left( {3a - 2} \right)^2} \ge 0,\forall a\) nên \(\left( {a - 1} \right){\left( {3a - 2} \right)^2} \le 0,\forall a \in \left( {0;1} \right)\). Tương tự, \(\begin{array}{l}\left( {b - 1} \right){\left( {3b - 2} \right)^2} \le 0,\forall b \in \left( {0;1} \right)\\\left( {c - 1} \right){\left( {3c - 2} \right)^2} \le 0,\forall c \in \left( {0;1} \right)\end{array}\) Do đó bđt trên luôn đúng với mọi \(a,b,c \in \left( {0;1} \right)\). Vậy \(21\left( {{a^2} + {b^2} + {c^2}} \right) \ge 20 + 9\left( {{a^3} + {b^3} + {c^3}} \right)\) (đpcm). HocTot.XYZ
|