Giải mục 1 trang 62, 63 SGK Toán 8 tập 2– Chân trời sáng tạoNêu nhận xét về hình dạng và kích thước của từng cặp hình:
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Video hướng dẫn giải Nêu nhận xét về hình dạng và kích thước của từng cặp hình: Hình 1a và Hình 1b, Hình 1c và Hình 1d, Hình 1e và Hình 1g.
Phương pháp giải: Quan sát và so sánh Lời giải chi tiết: Hình 1a và Hình 1b có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1a để thu được Hình 1b hoặc thu nhỏ Hình 1b để được Hình 1a. Hình 1c và Hình 1d có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1d để thu được Hình 1c hoặc thu nhỏ Hình 1c để được Hình 1d. Hình 1e và Hình 1g có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1e để thu được Hình 1g hoặc thu nhỏ Hình 1g để được Hình 1e. HĐ2 Video hướng dẫn giải Cho tam giác \(ABC\) và tam giác \(A'B'C'\) như Hình 2. a) Hãy viết các cặp góc bằng nhau. b) Tính và so sánh các tỉ số \(\frac{{A'B'}}{{AB}};\frac{{A'C'}}{{AC}};\frac{{B'C'}}{{BC}}\).
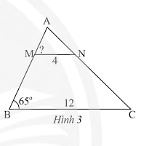
Phương pháp giải: Quan sát, so sánh, tính tỉ số. Lời giải chi tiết: a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là: \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\) b) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\). Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\) TH1 Video hướng dẫn giải Quan sát Hình 3, cho biết \(\Delta AMN\backsim\Delta ABC\). a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng. b) Tính góc \(\widehat {AMN}\).
Phương pháp giải: Hai tam giác đồng dạng với nhau thì các góc tương ứng bằng nhau và các cặp cạnh tương ứng có cùng tỉ lệ. Lời giải chi tiết: a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\) nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng) Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \) Vậy \(\widehat {AMN} = 65^\circ \).
|