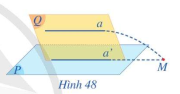
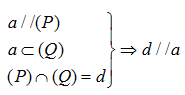Giải mục 2 trang 102, 103, 104 SGK Toán 11 tập 1 - Cánh DiềuCho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48).
Lựa chọn câu để xem lời giải nhanh hơn
HĐ2 Trả lời câu hỏi Hoạt động 2 trang 102 SGK Toán 11 Cánh diều Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’. a) Giả sử a cắt (P) tại M. Đường thẳng a có cắt đường thẳng a’ tại M hay không? b) Nêu vị trí tương đối của đường thẳng a và mặt phẳng (P). Vì sao?
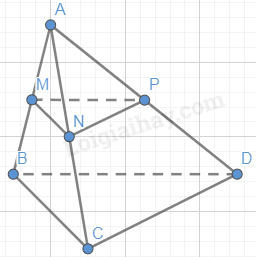
Phương pháp giải: Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P) Lời giải chi tiết: a) Đường thẳng a không cắt đường thẳng a’ tại M. b) Đường thẳng a và mặt phẳng (P) song song với nhau vì chúng không có điểm chung. LT-VD2 Trả lời câu hỏi Luyện tập - Vận dụng 2 trang 102 SGK Toán 11 Cánh diều Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao? Phương pháp giải: Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song (P). Lời giải chi tiết:
Tam giác ABC có: M, N là trung điểm của AB, AC. Suy ra MN // BC nên MN // (BCD). Tam giác ACD có: N, P là trung điểm của AC, AD. Suy ra NP // CD nên NP // (BCD). Tam giác ABD có: M, P là trung điểm của AB, AD. Suy ra MP // BD nên MP // (BCD). HĐ3 Trả lời câu hỏi Hoạt động 3 trang 102 SGK Toán 11 Cánh diều Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyển b. (Hình 51). a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không? b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?
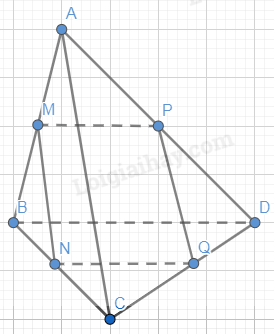
Phương pháp giải: Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a. Lời giải chi tiết: a) Đường thẳng a không cắt mặt phẳng (P) tại M. b) Hai đường thẳng a và b song song với nhau. LT-VD3 Trả lời câu hỏi Luyện tập - Vận dụng 3 trang 103 SGK Toán 11 Cánh diều Ở Ví dụ 3, xác định giao tuyến của mặt phẳng (R) với các mặt phẳng (ABD), (BCD), (ACD). Phương pháp giải: Dùng định lý 2.
Dùng hệ quả 2.
Lời giải chi tiết:
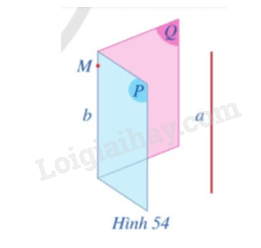
Ta có: M là giao điểm của (R) và (ABD). Mà (R) // BD. Từ M kẻ MP // BD và cắt AD tại P. Suy ra MP là giao tuyến của (R) và (ABD). Từ M kẻ MN // AC, cắt BC tại N. Do đó, N là giao điểm của (R) và (BCD). Từ N kẻ Nx // BD, cắt CD tại Q. Suy ra NQ là giao tuyển của (R) và (BCD). Ta có P là giao điểm của (R) và (ACD). Từ P kẻ PH // AC, cắt CD tại H. Suy ra PH là giao tuyến của (R) và (ACD). HĐ4 Trả lời câu hỏi Hoạt động 4 trang 103 SGK Toán 11 Cánh diều Cho hai mặt phẳng (P), (Q) cùng song song với đường thẳng a và (P) ∩ (Q) = b (Hình 54).
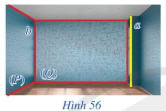
a) Lấy một điểm M trên đường thẳng b. Gọi b’, b” lần lượt là các giao tuyến của mặt phẳng (M, a) với (P) và mặt phẳng (M, a) với (Q). Cho biết b’ và b” có trùng với b hay không. b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao? Phương pháp giải: a) Chứng minh b', b'' đi qua điểm M và b // b' // b'' nên b' và b'' trùng với b. b) Vì a // b' nên a // b. Lời giải chi tiết: a) • Ta có: M ∈ b và (P) ∩ (Q) = b; Suy ra M ∈ (P). Mà M ∈ (M, a) Do đó M là giao điểm của (P) và (M, a). Lại có b’ = (P) ∩ (M, a) Suy ra đường thẳng b’ đi qua M. Tương tự ta cũng chứng minh được b’’ đi qua điểm M. • Ta có: a // (P); a ⊂ (M, a) (M, a) ∩ (P) = b’ Do đó a // b’. Tương tự ta cũng có a // b’’. Do đó b’ // b’’. Mặt khác: (P) ∩ (Q) = b; (M, a) ∩ (P) = b’; (M, a) ∩ (Q) = b’’; b // b’’. Do đó b // b’ // b’’. Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau. b) Vì a // b’ nên a // b (do b ≡ b’). LT-VD4 Trả lời câu hỏi Luyện tập - Vận dụng 4 trang 104 SGK Toán 11 Cánh diều Trong Hình 56, hai mặt tường của căn phòng gợi nên hình ảnh hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến b, mép cột gợi nên hình ảnh đường thẳng a. Cho biết đường thẳng a có song song với giao tuyến b hay không.
Phương pháp giải: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó. Lời giải chi tiết: Đường thẳng a song song với giao tuyến b.
|