Giải mục 2 trang 71 SGK Toán 9 tập 2 - Chân trời sáng tạoCho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4). a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp (widehat {DAB}) và (widehat {DCB}) b) Tính tổng số đo của các cung vừa tìm được. c) Nêu kết luận về tổng số đo của hai góc (widehat {DAB}) và (widehat {DCB}). d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
Lựa chọn câu để xem lời giải nhanh hơn
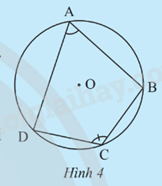
HĐ2 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 2 trang 71 SGK Toán 9 Chân trời sáng tạo Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4). a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp \(\widehat {DAB}\) và \(\widehat {DCB}\) b) Tính tổng số đo của các cung vừa tìm được. c) Nêu kết luận về tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\). d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
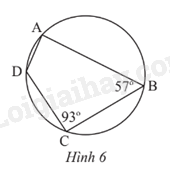
Phương pháp giải: - Dựa vào tính chất của số đo góc nội tiếp bằng \(\frac{1}{2}\) số đo cung bị chắn. - Dựa vào tổng các góc của tứ giác bằng 360o. Lời giải chi tiết: a) Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ. Góc \(\widehat {DCB}\) là góc nội tiếp chắn cung BD lớn. b) số đo cung BD nhỏ + số đo cung BD lớn = 360o c) - Góc \(\widehat {DAB}\) là góc nội tiếp chắn cung BD nhỏ. Suy ra \(\widehat {DAB} = \frac{1}{2}\) số đo cung BD nhỏ. - Góc \(\widehat {DCB}\) là góc nội tiếp chắn cung BD lớn. Suy ra \(\widehat {DCB} = \frac{1}{2}\) số đo cung BD lớn. Ta có \(\widehat {DAB} + \widehat {DCB} = \frac{1}{2}\) (số đo cung BD nhỏ + số đo cung BD lớn) = \(\frac{1}{2}\).360o = 180o. d) Tổng số đo của hai góc đối diện còn lại của tứ giác ABCD là 180o (vì 360o – 180o = 180o). TH2 Video hướng dẫn giải Trả lời câu hỏi Thực hành 2 trang 71 SGK Toán 9 Chân trời sáng tạo Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6.
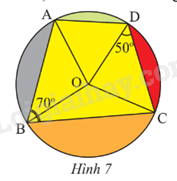
Phương pháp giải: Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o. Lời giải chi tiết: Tứ giác ABCD là tứ giác nội tiếp. Do đó \(\widehat A + \widehat C = {180^o}\) suy ra \(\widehat A = {180^o} - \widehat C = {180^o} - {93^o} = {87^o}\). \(\widehat B + \widehat D = {180^o}\) suy ra \(\widehat D = {180^o} - \widehat B = {180^o} - {57^o} = {123^o}\). VD2 Video hướng dẫn giải Trả lời câu hỏi Vận dụng 2 trang 71 SGK Toán 9 Chân trời sáng tạo Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết \(\widehat {ABC}\) = 70o, \(\widehat {OCD}\) = 50o. Tìm góc \(\widehat {AOD}\).
Phương pháp giải: Dựa vào: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o. Lời giải chi tiết: Tứ giác ABCD là tứ giác nội tiếp. Do đó \(\widehat {ABC} + \widehat {ADC} = {180^o}\) suy ra \(\widehat {ADC} = {180^o} - \widehat {ABC} = {180^o} - {70^o} = {110^o}\). Mà \(\widehat {ADO} + \widehat {OCD} = \widehat {ADC}\) suy ra \(\widehat {ADO} = {110^o} - {50^o} = {60^o}\). Vì OA = OD = R nên tam giác OAD cân tại O Suy ra \(\widehat {OAD} = \widehat {ADO} = {60^o}\) (tính chất tam giác cân) Vậy tam giác OAD đều suy ra \(\widehat {AOD} = {60^o}\).
|