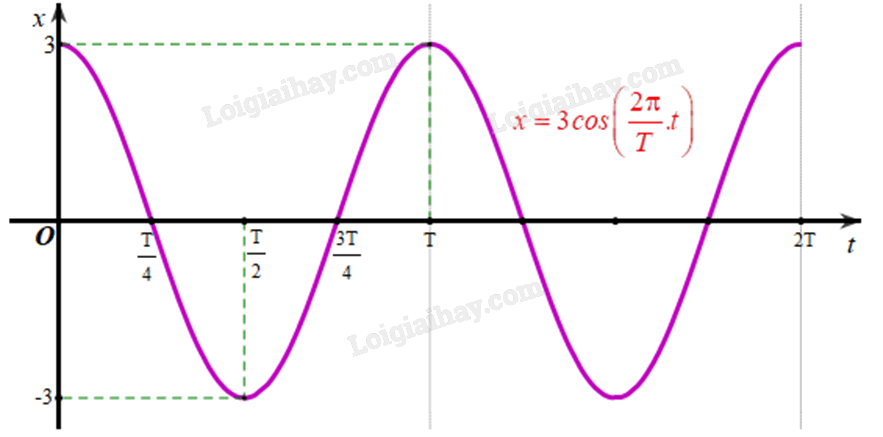
Bài 6 trang 31 SGK Toán 11 tập 1 - Cánh diềuMột dao động điều hòa có phương trình li độ dao động là: (x = Acos left( {omega t + varphi } right)), Đề bài Một dao động điều hoà có phương trình li độ dao động là: \(x = A \cos(\omega t + \varphi)\), trong đó \(A, \varphi, \omega\) là các hằng số (\(\omega > 0\)). Khi đó, chu kì \(T\) của dao động là \(T = \frac{2\pi}{\omega}\). a) Xác định giá trị của li độ khi \(t = 0\), \(t = \frac{T}{4}\), \(t = \frac{T}{2}\), \(t = \frac{3T}{4}\), \(t = T\). b) Vẽ đồ thị biểu diễn li độ của dao động điều hòa trên đoạn \([0; 2\pi]\) trong mỗi trường hợp sau: \(A = 3\) và \(\varphi = 0\); \(A = 3\) và \(\varphi = -\frac{\pi}{2}\); \(A = 3\) và \(\varphi = \pi\). Phương pháp giải - Xem chi tiết Thay các giá trị vào phương trình li độ để tính. Lời giải chi tiết a) \(T = \frac{{2\pi }}{\omega } \Leftrightarrow \omega = \frac{{2\pi }}{T}\). +) Với \(t = 0\) thì \(x = A\cos \left( {0 + \varphi } \right) = A\cos \varphi \). +) Với \(t = \frac{T}{4}\) thì \(x = A\cos \left( {\frac{{2\pi }}{T}.\frac{T}{4} + \varphi } \right) = A\cos \left( {\frac{\pi }{2} + \varphi } \right)\). +) Với \(t = \frac{T}{2}\) thì \(x = A\cos \left( {\frac{{2\pi }}{T}.\frac{T}{2} + \varphi } \right) = A\cos \left( {\pi + \varphi } \right)\). +) Với \(t = \frac{{3T}}{4}\) thì \(x = A\cos \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4} + \varphi } \right) = A\cos \left( {\frac{{3\pi }}{2} + \varphi } \right)\). +) Với \(t = T\) thì \(x = A\cos \left( {\frac{{2\pi }}{T}.T + \varphi } \right) = A\cos \left( {2\pi + \varphi } \right) = A\cos \varphi \). b) \(A = 3\), \(\varphi = 0\). +) Với t = 0 thì \(x = 3\cos \left( {\omega .0 + 0} \right) = 3\). +) Với \(t = \frac{T}{4}\) thì \(x = 3\cos \left( {\frac{\pi }{2} + 0} \right) = 0\). +) Với \(t = \frac{T}{2}\) thì \(x = 3\cos \left( {\pi + 0} \right) = - 3\). +) Với \(t = \frac{{3T}}{4}\) thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + 0} \right) = 0\). +) Với \(t = T\) thì \(x = 3\cos \left( {2\pi + 0} \right) = 3\).
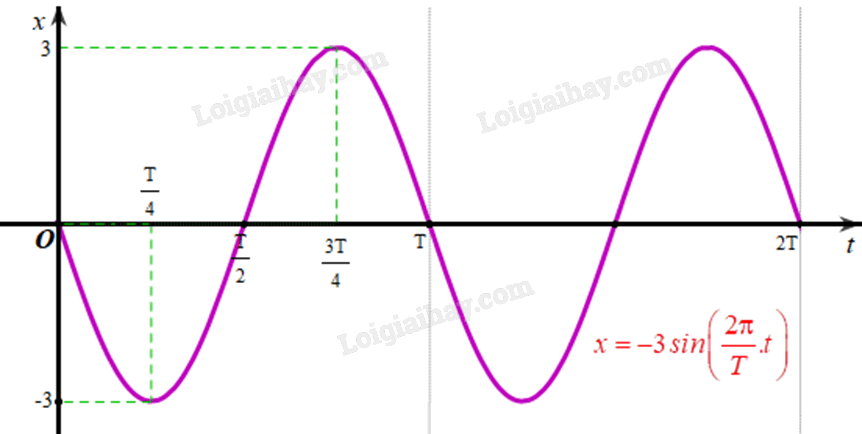
\(A = 3\), \(\varphi = - \frac{\pi }{2}\). +) Với t = 0 thì \(x = 3\cos \left( {0 - \frac{\pi }{2}} \right) = 0\). +) Với \(t = \frac{T}{4}\) thì \(x = 3\cos \left( {\frac{\pi }{2} - \frac{\pi }{2}} \right) = 3\). +) Với \(t = \frac{T}{2}\) thì \(x = 3\cos \left( {\pi - \frac{\pi }{2}} \right) = 0\). +) Với \(t = \frac{{3T}}{4}\) thì \(x = 3\cos \left( {\frac{{3\pi }}{2} - \frac{\pi }{2}} \right) = -3\). + Với \(t = T\) thì \(x = 3\cos \left( {2\pi - \frac{\pi }{2}} \right) = 0\).
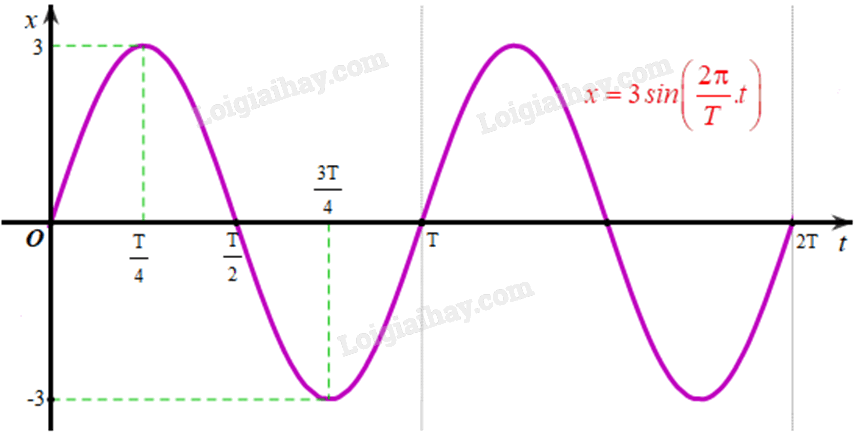
\(A = 3\), \(\varphi = \frac{\pi }{2}\). +) Với t = 0 thì \(x = 3\cos \left( {0 + \frac{\pi }{2}} \right) = 0\). +) Với \(t = \frac{T}{4}\) thì \(x = 3\cos \left( {\frac{\pi }{2} + \frac{\pi }{2}} \right) = -3\). +) Với \(t = \frac{T}{2}\) thì \(x = 3\cos \left( {\pi + \frac{\pi }{2}} \right) = 0\). +) Với \(t = \frac{{3T}}{4}\) thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + \frac{\pi }{2}} \right) = 3\). + Với \(t = T\) thì \(x = 3\cos \left( {2\pi + \frac{\pi }{2}} \right) = 0\).
|