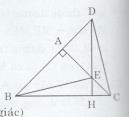
Bài tập 28 trang 123 Tài liệu dạy – học Toán 7 tập 2Giải bài tập Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh: GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.XYZ và nhận về những phần quà hấp dẫn Đề bài Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh: a) DE vuông góc với BC. b) BE vuông góc với DC. Lời giải chi tiết
a) Gọi H là giao điểm của DE và BC. Ta có: ^ADE+^AED=90∘ (∆ADE vuông tại A) ^ADE=^ECH(=45∘) ^AED=^HEC (hai góc đối đỉnh) Do đó: ^ECH+^HEC=90∘ Mà ^ECH+^HEC+^EHC=180∘ (tổng ba góc trong một tam giác) Nên 90∘+^EHC=180∘⇒^EHC=90∘⇒EH⊥BC⇒DE⊥BC. b) ∆BDC có: DE là đường cao (DE⊥BC), CA là đường cao (CA⊥AB,D∈BA) và DE cắt CA tại E (gt) Do đó E là trực tâm của ∆BDC. Vậy BE là đường cao của tam giác ABC. Nên BE⊥DC. HocTot.XYZ  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
