Đề thi học kì 1 Toán 9 - Đề số 4Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{4x - y = 2}\\{x + 3y = 7}\end{array}} \right.\) . Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
Câu 2 :
Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x - 4}} + 1 = \frac{1}{{x + 3}}\)
Câu 3 :
Số 3 là nghiệm của bất phương trình nào sau đây?
Câu 4 :
Số nào sau đây có căn bậc hai số học bằng 4?
Câu 5 :
Căn thức \(\sqrt {4 - 2x} \) xác định khi
Câu 6 :
Sau khi rút gọn biểu thức \(\frac{2}{{2 - \sqrt 3 }} + \frac{2}{{2 + \sqrt 3 }}\) ta được phân số tối giản \(\frac{a}{b}\), giá trị \(a + b\) là
Câu 7 :
Giá trị của biểu thức \(A = \sqrt {25} .\sqrt 9 - \sqrt[3]{{ - 27}}\) là
Câu 8 :
Tam giác ABC vuông tại A có AC = 6cm; BC = 12cm. Số đo góc ACB bằng
Câu 9 :
Dây lớn nhất của đường tròn \(\left( {O;3cm} \right)\) có độ dài bằng
Câu 11 :
Tỉ số giữa độ dài cung \(n^\circ \) và độ dài đường tròn (cùng bán kính) bằng
Câu 12 :
Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Khi đó
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{4x - y = 2}\\{x + 3y = 7}\end{array}} \right.\) . Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
Đáp án : C Phương pháp giải :
Giải hệ phương trình hoặc sử dụng máy tính cầm tay để tính nghiệm của hệ phương trình. Lời giải chi tiết :
Sử dụng máy tính cầm tay, ta tính được nghiệm của hệ phương trình là \(\left( {1;2} \right)\).
Đáp án C
Câu 2 :
Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x - 4}} + 1 = \frac{1}{{x + 3}}\)
Đáp án : C Phương pháp giải :
Điều kiện xác định của phương trình chứa ẩn ở mẫu là mẫu thức khác 0. Lời giải chi tiết :
Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x - 4}} + 1 = \frac{1}{{x + 3}}\) là \(x - 4 \ne 0\) và \(x + 3 \ne 0\). Suy ra \(x \ne 4\) và \(x \ne - 3\). Đáp án C
Câu 3 :
Số 3 là nghiệm của bất phương trình nào sau đây?
Đáp án : B Phương pháp giải :
Thay \(x = 3\) vào các bất đẳng thức để xác định. Lời giải chi tiết :
Với \(x = 3\) thì \(5.3 - 10 = 15 > 0\) nên \(x = 3\) không phải nghiệm của \(5x - 10 \le 0\). Với \(x = 3\) thì \(2.3 + 1 = 7 > 0\) nên \(x = 3\) là nghiệm của \(2x + 1 > 0\). Với \(x = 3\) thì \( - 5.3 + 7 = - 8 < 0\) nên \(x = 3\) không phải nghiệm của \( - 5x + 7 \ge 0\). Với \(x = 3\) thì \(2.3 - 5 = 1 > 0\) nên \(x = 3\) không phải nghiệm của \(2x - 5 < 0\). Đáp án B
Câu 4 :
Số nào sau đây có căn bậc hai số học bằng 4?
Đáp án : D Phương pháp giải :
Số \(x\) có căn bậc hai số học bằng a thì \(x = {a^2}\). Lời giải chi tiết :
Số có căn bậc hai số học bằng 4 là \({4^2} = 16\). Đáp án D
Câu 5 :
Căn thức \(\sqrt {4 - 2x} \) xác định khi
Đáp án : B Phương pháp giải :
Căn thức \(\sqrt A \) xác định khi \(A \ge 0\). Lời giải chi tiết :
Căn thức \(\sqrt {4 - 2x} \) xác định khi \(4 - 2x \ge 0\) suy ra \(x \le 2\). Đáp án B
Câu 6 :
Sau khi rút gọn biểu thức \(\frac{2}{{2 - \sqrt 3 }} + \frac{2}{{2 + \sqrt 3 }}\) ta được phân số tối giản \(\frac{a}{b}\), giá trị \(a + b\) là
Đáp án : B Phương pháp giải :
Rút gọn biểu thức bằng cách trục căn thức, sau đó tính tổng a + b. Lời giải chi tiết :
\(\frac{2}{{2 - \sqrt 3 }} + \frac{2}{{2 + \sqrt 3 }} = \frac{{2\left( {2 + \sqrt 3 } \right) + 2\left( {2 - \sqrt 3 } \right)}}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} = \frac{{4 + 2\sqrt 3 + 4 - 2\sqrt 3 }}{{4 - 3}} = \frac{8}{1}\). Suy ra \(a + b = 8 + 1 = 9\). Đáp án B
Câu 7 :
Giá trị của biểu thức \(A = \sqrt {25} .\sqrt 9 - \sqrt[3]{{ - 27}}\) là
Đáp án : C Phương pháp giải :
Sử dụng tính chất của căn bậc hai, căn bậc ba để tính. Lời giải chi tiết :
\(A = \sqrt {25} .\sqrt 9 - \sqrt[3]{{ - 27}} = 5.3 - \left( { - 3} \right) = 15 + 3 = 18\) Đáp án C
Câu 8 :
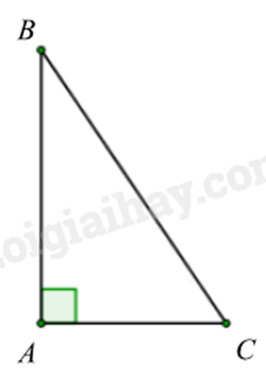
Tam giác ABC vuông tại A có AC = 6cm; BC = 12cm. Số đo góc ACB bằng
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về tỉ số lượng giác và tìm số đo góc khi biết tỉ số lượng giác. Lời giải chi tiết :
Áp dụng hệ thức lượng trong tam giác vuông vào tam giác ABC, ta có: \(\cos ACB = \frac{{AC}}{{BC}} = \frac{6}{{12}} = \frac{1}{2}\) suy ra \(\widehat {ACB} = 60^\circ \). Đáp án C
Câu 9 :
Dây lớn nhất của đường tròn \(\left( {O;3cm} \right)\) có độ dài bằng
Đáp án : B Phương pháp giải :
Trong một đường tròn, đường kính là dây cung lớn nhất. Lời giải chi tiết :
Dây lớn nhất của đường tròn là đường kính, do đó độ dài là 3.2 = 6cm. Đáp án B
Đáp án : C Phương pháp giải :
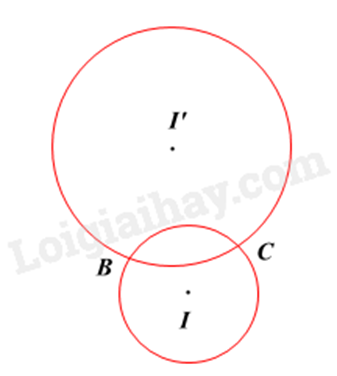
Quan sát hình vẽ để xác định. Lời giải chi tiết :
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) có hai điểm chung nên chúng cắt nhau. Đáp án C
Câu 11 :
Tỉ số giữa độ dài cung \(n^\circ \) và độ dài đường tròn (cùng bán kính) bằng
Đáp án : A Phương pháp giải :
Sử dụng công thức tính độ dài cung tròn và độ dài đường tròn. Độ dài cung tròn \(n^\circ \): \(l = \frac{{n\pi R}}{{180}}\) Độ dài đường tròn: \(C = 2\pi R\) Lời giải chi tiết :
Tỉ số giữa độ dài cung \(n^\circ \) và độ dài đường tròn (cùng bán kính) bằng: \(\frac{l}{C} = \frac{{n\pi R}}{{180}}:2\pi R = \frac{{n\pi R}}{{360\pi R}} = \frac{n}{{360}}\). Đáp án A
Câu 12 :
Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Khi đó
Đáp án : A Phương pháp giải :
Sử dụng định lí Pythagore đảo và tính chất tiếp tuyến để kiểm tra. Lời giải chi tiết :
Tam giác ABC có: \(A{B^2} + A{C^2} = {3^2} + {4^2} = {5^2} = B{C^2}\) nên tam giác ABC vuông tại A (theo định lí Pythagore đảo). Suy ra AB vuông góc với AC tại A. Mà A thuộc đường tròn (B; AB) hay (B; 3). Do đó AC là tiếp tuyến của đường tròn (B; 3). Đáp án A
II. Tự luận
Phương pháp giải :
a) Rút gọn phân thức trước rồi rút gọn biểu thức. b) Thay \(x = 16\) vào P để tính giá trị. c) Tìm M thay vào \({M^2} < \frac{1}{4}\) để tìm x, lưu ý điều kiện đầu bài. Lời giải chi tiết :
a) Ta có: \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{x - 2\sqrt x }}{{x - 4}}\) \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{\sqrt x \left( {\sqrt x {\rm{\;}} - 2} \right)}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} + 2} \right)}}\) \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}\) \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}\). b) Thay \(x = 16\) vào P, ta được: \(P = \frac{{\sqrt {16} }}{{\sqrt {16} - 2}} = \frac{4}{{4 - 2}} = \frac{4}{2} = 2\). Vậy với \(x = 16\) thì \(P = 2\). c) Ta có: \(M = P:Q = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}:\frac{{\sqrt x {\rm{\;}} + 2}}{{\sqrt x {\rm{\;}} - 2}}{\mkern 1mu} \) \( = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}.\frac{{\sqrt x {\rm{\;}} - 2}}{{\sqrt x {\rm{\;}} + 2}} = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}\) Vì \({M^2} < \frac{1}{4}\) nên \({\left( {\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}} \right)^2} < \frac{1}{4}\). Suy ra \(\left| {\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}} \right| < \frac{1}{2}\) Vì \(\sqrt x > 0\) nên \(\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} > 0\) Do đó \(\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} < \frac{1}{2}\) \(2\sqrt x {\rm{\;}} < \sqrt x {\rm{\;}} + 2\) \(\sqrt x {\rm{\;}} < 2\) \(x < 4\) Kết hợp điều kiện \(x \ge 0;x \ne 4\) ta được \(0 \le x < 4\). Vậy để \({M^2} < \frac{1}{4}\) thì \(0 \le x < 4\). Phương pháp giải :
Gọi số tiền đầu tư cho mỗi khoản lần lượt là \(x,y\) (\(x,y \in {\mathbb{N}^*};x,y \le 630\) ) Lập hệ phương trình với x và y. Từ đó giải hệ phương trình. Lời giải chi tiết :
Gọi số tiền đầu tư cho mỗi khoản lần lượt là \(x,y\) (\(x,y \in {\mathbb{N}^*};x,y \le 630\) ) Vì bác An chia số tiền \(630\) triệu đồng của mình cho hai khoản đầu tư nên \(x + y = 630\) (triệu đồng) Vì lợi nhuận của khoản đầu tư thứ nhất là \(10\% \), lợi nhuận của khoản đầu tư thứ hai là \(30\% \) và sau một năm lợi nhuận thu về là \(157\) triệu đồng nên \(10\% x + 30\% y = 157\) hay \(0,1x + 0,3y = 157\) Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{0,1x + 0,3y = 157}\end{array}} \right.\) Giải hệ phương trình: \(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{0,1x + 0,3y = 157}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{x + 3y = 1570}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{2y = 940}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{y = 470}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x = 160(TM)}\\{y = 470(TM)}\end{array}} \right.\end{array}\) Vậy khoản đầu tư thứ nhất là \(160\) triệu đồng, khoản đầu tư thứ hai là \(470\) triệu đồng. Phương pháp giải :
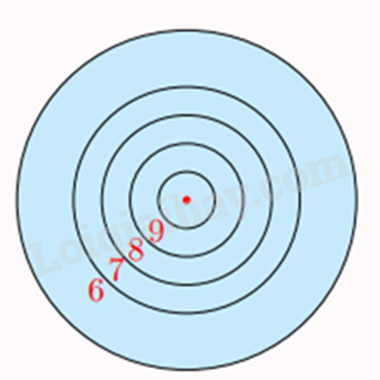
Sử dụng công thức tính diện tích hình vành khuyên để tính diện tích hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai: \({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\) với \(R > r\). Sử dụng công thức tính diện tích hình tròn để tính diện tích hình tròn lớn nhất: \(S = \pi {r^2}\) Tính tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất Lời giải chi tiết :
Vì bán kính của đường tròn thứ nhất và thứ hai lần lượt là 5cm và 10cm nên diện tích hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai là: \({S_{vk}} = \pi \left( {{{10}^2} - {5^2}} \right) = 75\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\) Vì hình tròn lớn nhất có bán kính là 30cm nên diện tích hình tròn lớn nhất: \(S = {30^2} \cdot \pi = 900\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\) Xác suất ném trúng vòng 9 là: \(\frac{{{S_{vk}}}}{S} = \frac{{75\pi }}{{900\pi }} = \frac{1}{{12}}\) Vậy xác suất ném trúng vòng 9 là \(\frac{1}{{12}}\). Phương pháp giải :
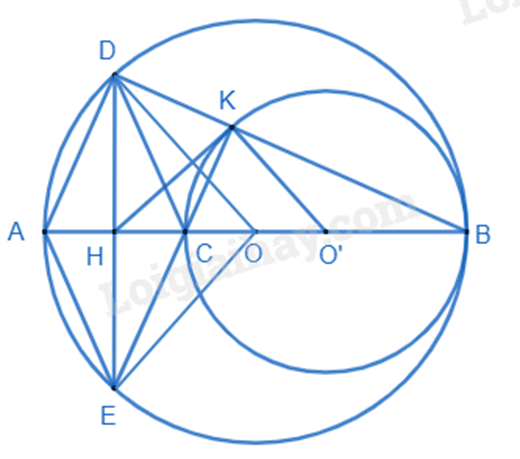
a) Chứng minh \(\Delta ODH = \Delta OEH\left( {ch - cgv} \right)\) suy ra DH = HE Tứ giác có hai đường chéo vuông góc tại trung điểm của mỗi đường là hình thoi. b) Chứng minh \(EC \bot DB\) và \(CK \bot DB\) nên E, C, K thẳng hàng (tiên đề Euclid). c) Chứng minh \(\widehat {HKE} = \widehat {HEK}\) và \(\widehat {O'KC} = \widehat {HCE}\), suy ra \(\widehat {HKE} + \widehat {O'KC} = 90^\circ \) nên \(\widehat {HKO'} = 90^\circ \). Lời giải chi tiết :
a) Xét \(\Delta ODH\) và \(\Delta OEH\) có: \(\begin{array}{l}\widehat {OHD} = \widehat {OHE} = 90^\circ \\OD = OE = R\\OH\,{\rm{chung}}\end{array}\) Suy ra \(\Delta ODH = \Delta OEH\left( {ch - cgv} \right)\) Do đó DH = HE (hai cạnh tương ứng). Mà \(H \in DE\) suy ra H là trung điểm của BE. Tứ giác ADCE có H là trung điểm của hai đường chéo DE, AC và \(AC \bot DE\) tại H nên tứ giác ADCE là hình thoi. b) Ta có \(AD \bot DB\) (Vì AB là đường kính của \((O)\) và \(D \in (O)\)) nên suy ra \(EC \bot DB\) (1) (Vì tứ giác ADCE là hình thoi). Lại có \(CK \bot KB\) (Vì CB là đường kính của \((O')\) và \(K \in (O')\)) hay \(CK \bot DB\) (2). Từ (1) và (2) suy ra E, C, K thẳng hàng (tiên đề Euclid). c) Xét \(\Delta DKE\) vuông tại K có KH là đường trung tuyến ứng với cạnh huyền nên \(HK = HE = \frac{1}{2}DE\). Suy ra \(\Delta HKE\) cân tại H, do đó \(\widehat {HKE} = \widehat {HEK}\). Lại có \(\widehat {O'KC} = \widehat {O'CK}\) (tam giác O’CK cân tại O’) và \(\widehat {O'CK} = \widehat {HCE}\) (2 góc đối đỉnh) do đó \(\widehat {O'KC} = \widehat {HCE}\). Mà \(\widehat {HEK} + \widehat {HCE} = 90^\circ \) (hai góc phụ nhau) nên \(\widehat {HKE} + \widehat {O'KC} = 90^\circ \), suy ra \(\widehat {HKO'} = 90^\circ \) Do đó \(HK \bot KO'\). Vậy HK là tiếp tuyến của \((O')\) tại K . Phương pháp giải :
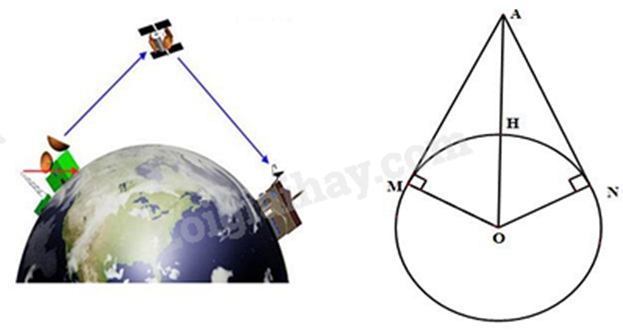
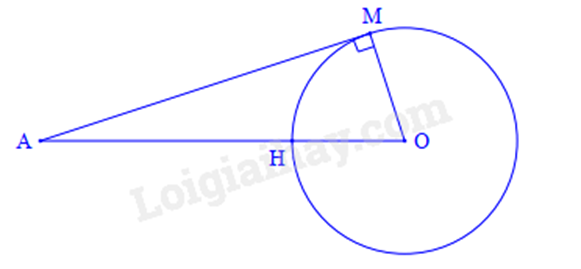
Khoảng cách từ vệ tính đến mặt đất chính là độ dài của đoạn AM hoặc AN. Ta cần sử dụng công thức \(S = vt\), trong đó S là quãng đường truyền tín hiệu đi được trong khoảng thời gian t. Xác định thời gian tín hiệu truyền từ A đến M. Lời giải chi tiết :
Do thời gian từ lúc truyền tín hiệu đến lúc nhận lại tín hiệu là 0,28s, nên thời gian tín hiệu truyền từ A đến M là: \(0,28:2 = 0,14\left( s \right)\) Độ dài đoạn AM cũng là quãng đường tín hiệu truyền đi được trong 0,14s là: \(S = AM = vt = {3.10^8}.0,14 = 42\,000\,000\left( m \right) = 42\,000\left( {km} \right)\) Vị trí xa nhất trên trái đất có thể nhận tín hiệu từ vệ tinh là vô số điểm M (với AM là tiếp tuyến kẻ từ A đến đường tròn tâm O). Vì AM là tiếp tuyến (O) nên \(OM \bot AM\) tại M. Áp dụng định lý Pythagore vào tam giác vuông AMO ta có: \(O{A^2} = O{M^2} + M{A^2} = 6\,{400^2} + 42\,{000^2} = 1\,804\,960\,000\) Suy ra \(OA = \sqrt {1\,804\,960\,000} = 42\,485\left( {km} \right)\). Khoảng cách từ vệ tinh Vinasat-1 đến mặt đất là độ dài đoạn AH: \(AH = AO - OH = 42\,485 - 6\,400 = 36\,085\left( {km} \right)\).
|