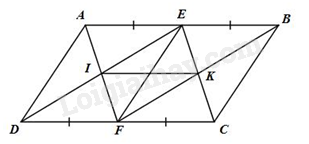
Giải bài 11 trang 89 SGK Toán 8 tập 1– Chân trời sáng tạo

Đề bài

Cho hình bình hành $ABCD$ có $AB = 2AD$. Gọi $E$ và $F$ lần lượt là trung điểm của $DF$ và $CD$, $I$ là giao điểm của $AF$ và $DE$, $K$ là giao điểm của $BF$ và $CE$

a) Chứng minh rằng tứ giác $AECF$ là hình bình hành

b) Tứ giác $AEFD$ là hình gì? Vì sao?

c) Chứng minh tứ giác $EIFK$ là hình chữ nhật

d) Tìm điều kiện của hình bình hành $ABCD$ để tứ giác $EIFK$ là hình vuông

Lời giải chi tiết

a) Ta có:

$AE = EB = \frac{1}{2}AB$ (do $E$ là trung điểm của $AB$)

$DF = FC = \frac{1}{2}CD$ ($F$ là trung điểm của $CD$)

$AB = CD$ (do $ABCD$ là hình bình hành)

Suy ra $AE = CF = EB = DF$

Xét tứ giác $AECF$ ta có:

$AE$ // $CF$ (do $AB$ // $CD$)

$AE = CF$

Suy ra $AECF$ là hình bình hành

b) Vì $AB = 2AD$ (gt) và $AB = 2AE$  (do $E$ là trung điểm của $AB$)

Suy ra $AD = AE$

Xét tứ giác $AEFD$ có $AE$ // $DF$ và $AE = DF$ (cmt)

Suy ra $AEFD$ là hình bình hành

Mà $AE = AD$ (cmt)

Suy ra $AEFD$ là hình thoi

c) Ta có $AF \bot DE$ (do $AEFD$ là hình thoi)

và $AF$ // $EC$ ($AECF$ là hình bình hành)

Suy ra $EC \bot DE$

Suy ra $\widehat {IEK} = 90^\circ$

Vì $AEFD$ là hình thoi nên $EF = AE$

Và $AE = \frac{1}{2}AB$ (gt)

Suy ra $EF = \frac{1}{2}AB$

Xét $\Delta AFB$ có $FE$ là đường trung tuyến và $EF = \frac{1}{2}AB$

Suy ra $\Delta AFB$ vuông tại $F$

Suy ra $\widehat {{\rm{IFK}}} = 90$

Xét tứ giác $EIFK$ ta có:

$\widehat {{\rm{EIF}}} = 90$ (do $AF \bot DE$)

$\widehat {{\rm{IEK}}} = 90^\circ$ (cmt)

$\widehat {{\rm{IFK}}} = 90^\circ$ (cmt)

Suy ra $EIFK$ là hình chữ nhật

d) $EIFK$ là hình vuông

Suy ra $FI = EI$

Mà $EI = ID = \frac{1}{2}DE$ ( do $AEFD$ là hình thoi)

$FI = IA = \frac{1}{2}AF$  (do $AEFD$ là hình thoi)

Suy ra $AF = DE$

Mà $AEFD$ là hình thoi

Suy ra $AEFD$ là hình chữ nhật

Suy ra $\widehat {{\rm{ADC}}} = 90^\circ$

Mà $ABCD$ là hình bình hành (gt)

Suy ra $ABCD$ là hình chữ nhật

Vậy nếu hình bình hành $ABCD$ là hình chữ nhật thì $EIFK$ là hình vuông