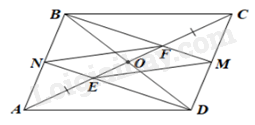
Giải bài 8 trang 89 SGK Toán 8 tập 1– Chân trời sáng tạo

Đề bài

Cho hình bình hành $ABCD$. Các điểm $E$, $F$ thuộc đường chéo $AC$ sao cho $AE = EF = FC$. Gọi $M$ là trung điểm của $BF$ và $CD$, $N$ là giao điểm của $DE$ và $AB$. Chứng minh rằng:

a) $M$, $N$ theo thứ tự là trung điểm của $CD$, $AB$

b) $EMFN$ là hình bình hành

Lời giải chi tiết

a) Ta có:

$AE = EF = FC$ nên $AE = EF = FC = \frac{1}{3}AC$ (1)

Vì $ABCD$ là hình bình hành (gt)

Suy ra $O$ là trung điểm của $AC$ hay $OA = OC = \frac{1}{2}AC$ và $AC = 2OA = 2OC$ (2)

Từ (1) và (2) suy ra $AE = EF = FC = \frac{2}{3}OA = \frac{2}{3}OC$.

Xét $\Delta BCD$ có $CO$ là trung tuyến và $CF = \frac{2}{3}CO$ (cmt)

Suy ra $F$ là trọng tâm của $\Delta BCD$

Suy ra $BM$ là đường trung tuyến của $\Delta BCD$

Suy ra $M$ là trung điểm của $CD$

Xét $\Delta ABD$ có $AO$ là trung tuyến và $AE = \frac{2}{3}AO$ (cmt)

Suy ra $E$ là trọng tâm của $\Delta ABD$

Suy ra $DN$ là đường trung tuyến của $\Delta ABD$

Suy ra $N$ là trung điểm của $AB$

b) Do M là trung điểm của CD (câu a) nên $MC = MD = \frac{1}{2}CD$.

            N là trung điểm của AB (câu a) nên $NB = NA = \frac{1}{2}AB$.

Mà AB = CD và AB // CD (do ABCD là hình bình hành)

Suy ra NB = MD và NB // MD.

Xét tứ giác BMDN có NB = MD và NB // MD

Do đó BMDN là hình bình hành.

Suy ra BM // DN và BM = DN.

Ta có E là trọng tâm của $\Delta$ABD nên  $EN = \frac{1}{3}DN$.

F là trọng tâm của $\Delta$BCD nên $FM = \frac{1}{3}BM$.

Mà DN = BM (chứng minh trên) nên EN = FM.

Xét tứ giác EMFN có EN = FM và EN // FM (do BM // DN)

Suy ra EMFN là hình bình hành.